Posizione e orientamento di un corpo rigido nello spazio
Per rappresentare un corpo rigido nello spazio tridimensionale è necessario determinarne la posa, cioè la combinazione di posizione e orientamento rispetto a un sistema di riferimento assegnato.
La posizione individua la collocazione di un punto caratteristico del corpo, mentre l’orientamento definisce la direzione degli assi solidali al corpo rispetto al riferimento esterno.
Considero un sistema di riferimento cartesiano ortonormale $ O - xyz$.
Un sistema di riferimento cartesiano ortonormale è formato da tre assi perpendicolari tra loro (x, y, z) che si intersecano in un punto detto origine. Gli assi hanno la stessa unità di misura e la stessa scala, perciò le coordinate di un punto rappresentano le sue distanze lungo direzioni mutuamente ortogonali. In questo modo è possibile descrivere con precisione la posizione di ogni punto nello spazio.
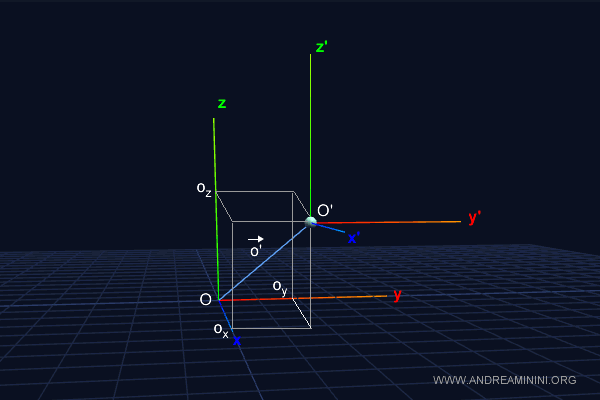
Per rappresentare il corpo rigido, associo a quest'ultimo un secondo sistema di riferimento $ O' - x'y'z' $, solidale al corpo.

L’origine $ O' $ del secondo sistema di riferimento viene utilizzata per specificare la posizione del corpo nelle coordinate $ x', y', z' $, mentre i versori $ \vec{x'} $, $ \vec{y'} $ e $ \vec{z'} $ descrivono l’orientamento del corpo.
La posizione di $ O' $ può essere espressa tramite le sue componenti lungo gli assi del riferimento fisso. Se indico con $ o' $ il vettore posizione di $O' $, questo può essere rappresentato nella forma:
$$ o' = \begin{bmatrix} o'_x \ o'_y \ o'_z \end{bmatrix} $$
Dove $ o'_x $, $ o'_y $ e $ o'_z $ sono le componenti del vettore lungo gli assi $ x $, $ y $ e $ z $ ossia nel primo sistema di riferimento.
Questa rappresentazione compatta riassume la posizione del corpo come traslazione rispetto all’origine del sistema di riferimento fisso.
Per descrivere l’orientamento, si osservi che ciascuno dei versori $ \vec{x'} $, $ \vec{y'} $ e $ \vec{z'} $ del sistema solidale al corpo (secondo sistema di riferimento) può essere espresso come combinazione lineare dei versori del riferimento fisso.
Introducendo i coseni direttori, l’orientamento può essere rappresentato dalle seguenti relazioni:
$$ x' = x'_x x + x'_y y + x'_z z $$
$$ y' = y'_x x + y'_y y + y'_z z $$
$$ z' = z'_x x + z'_y y + z'_z z $$
I coefficienti $ x'_x, x'_y, x'_z, \dots, z'_z $ individuano le componenti dei versori solidali al corpo rispetto alla base ortonormale $ (x, y, z) $ e costituiscono i coseni direttori degli assi del corpo rispetto al riferimento fisso.
Raccogliendo questi coefficienti in forma matriciale, posso rappresentare l’orientamento mediante una matrice di rotazione:
$$
R=
\begin{bmatrix}
x'_x & y'_x & z'_x \\
x'_y & y'_y & z'_y \\
x'_z & y'_z & z'_z
\end{bmatrix} $$
Questa matrice contiene nelle sue colonne i versori $ \vec{x'} $, $ \vec{y'} $ e $ \vec{z'} $ espressi nel sistema $ O - xyz $ (primo sistema).
Poiché i versori sono ortonormali, la matrice $ R $ è una matrice ortogonale con determinante pari a 1, condizione che caratterizza le matrici di rotazione e assicura che l’orientamento del corpo rigido sia descritto da una trasformazione che preserva angoli e distanze.
In questo modo, la posa del corpo rigido risulta completamente determinata dai due elementi fondamentali: il vettore posizione $ o' $ e la matrice di rotazione $ R $.
Questi consentono di esprimere la posizione e l’orientamento del corpo nello spazio in modo univoco e coerente rispetto al sistema di riferimento scelto.
Questa formalizzazione costituisce la base per lo studio della cinematica del corpo rigido e, più in generale, dei manipolatori robotici.
E così via.
