Algoritmo Naive Bayes

Naive Bayes è un algoritmo per risolvere problemi di classificazione e apprendimento automatico (machine learning) che utilizza il teorema di Bayes.

Cos'è un problema di classificazione? E' un algoritmo detto classificatore (classifier) che assegna una classe a ogni istanza di dati. Ad esempio, classificare se una email è spam oppure non spam.

Il teorema di Bayes mi permette di calcolare per ogni istanza la probabilità di appartenenza a una classe.

Cos'è il teorema di Bayes

Il teorema di Bayes calcola la probabilità di un evento A condizionata a un altro evento B. $$ P(A|B) = \frac{P(B|A) \cdot P(A) }{P(B)} $$

Si usa per calcolare la probabilità condizionata di un evento, in base alle informazioni disponibili su altri eventi correlati.

Come funziona l'algoritmo

Per spiegare il funzionamento dell'algoritmo faccio un esempio pratico.

Il problema consiste nel decidere se giocare a golf (oppure no) in base a determinate caratteristiche.

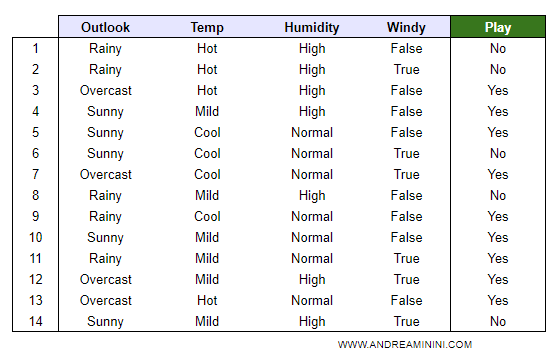
Le caratteristiche sono quattro: overcast (meteo), temp (temperatura), humidity (umidità), windy (forza del vento).

Per ogni caratteristica costruisco la tavola delle frequenze.

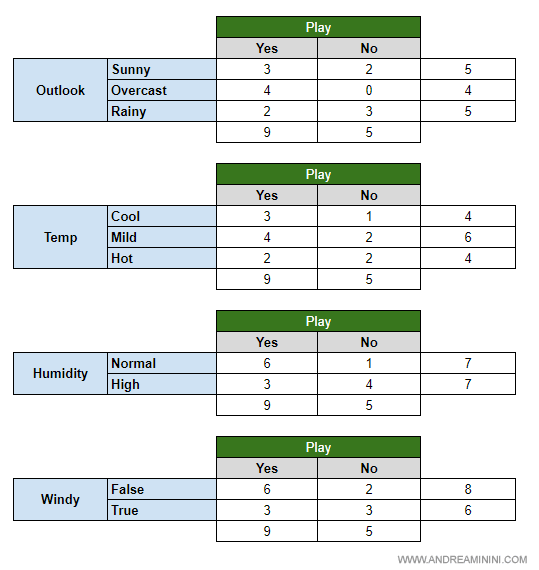
Poi trasformo le frequenze in probabilità.

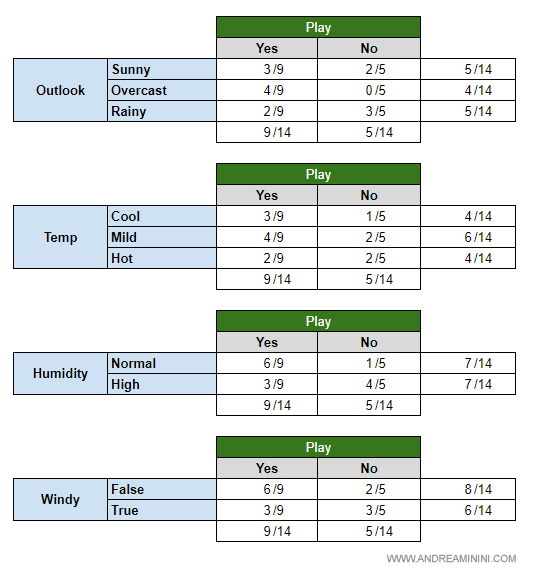
A questo punto, ho tutte le informazioni utili per calcolare le probabilità semplici e le probabilità condizionate.

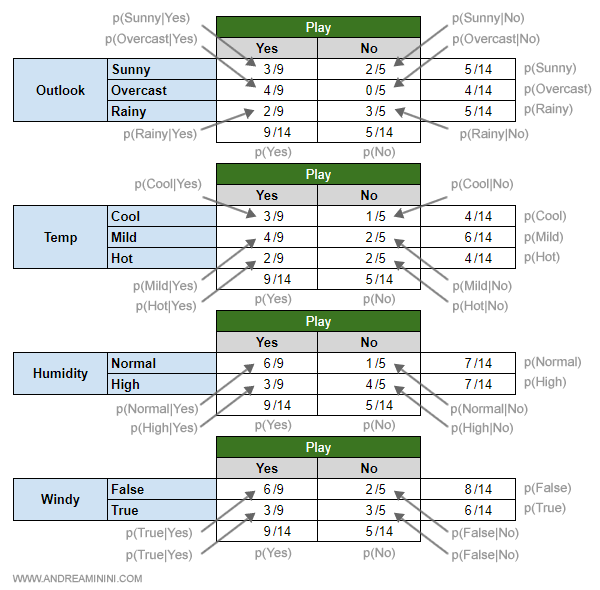
A questo punto il modello è pronto per essere utilizzato.

Ad esempio, se le condizioni di ambiente X sono le seguenti

• Outlook=Rainy
• Temp=Cool
• Humidity=High
• Windy=True

L'algoritmo calcola la probabilità della decisione di giocare, oppure no, moltiplicando tra loro le probabilità condizionali

$$ \begin{cases} P(Yes|X)=P(Rainy|Yes)·P(Cool|Yes)·P(High|Yes)·P(True|Yes)·P(Yes) \\ P(No|X)=P(Rainy|No)·P(Cool|No)·P(High|No)·P(True|No)·P(No) \end{cases} $$

Sostituisco i valori delle probabilità condizionate.

$$ \begin{cases} P(Yes|X)=(2/9)·(3/9)·(3/9)·(3/9)·(9/14) \\ P(No|X)=(3/5)·(1/5)·(4/5)·(3/5)·(5/14) \end{cases} $$

$$ \begin{cases} P(Yes|X)=0.00529 \\ P(No|X)=0.02057 \end{cases} $$

Infine, normalizzo i risultati

$$ \begin{cases} P(Yes|X)=\frac{0.00529}{0.00529+0.02057} \\ P(No|X)=\frac{0.02057}{0.00529+0.02057} \end{cases} $$

$$ \begin{cases} P(Yes|X)=0.20 \\ P(No|X)=0.80 \end{cases} $$

In conclusione, considerando le circostanze la probabilità di giocare è del 20%.

La probabilità opposta di non giocare è del 80%.

Pro e contro dell'algoritmo

I vantaggi

Dal punto di vista dei vantaggi l'algoritmo Naive Bayes ha la semplicità d'utilizzo.

Pur essendo un algoritmo semplice e datato, ancora oggi risolve egregiamente alcuni problemi di classificazione con una discreta efficienza.

Tuttavia, l'applicazione è limitata a pochi casi specifici.

Gli svantaggi

Dal punto di vista degli svantaggi vanno ricordati soprattutto i seguenti:

• L'algoritmo richiede la conoscenza di tutti i dati del problema. In particolar modo delle probabilità semplici e condizionate. Spesso sono informazioni difficili e costose da ottenere.
• L'algoritmo fornisce un'approssimazione "ingenua" (naive) del problema perché non considera la correlazione tra le caratteristiche dell'istanza.

E così via.