Regressione logistica
La regressione logistica è un algoritmo di apprendimento supervisionato che costruisce un modello probabilistico lineare di classificazione dei dati.
E' usata nel machine learning per l'addestramento di un algoritmo nella classificazione supervisionata dei dati.
La classificazione può essere binaria (due classi) o multiclasse (più classi).
La differenza tra regressione logistica e lineare. Il nome "regressione" deriva dal fatto che la formula della regressione logistica è simile alla formula matematica della regressione lineare. In ogni caso, va precisato che non sono la stessa cosa. La regressione logistica è un modello di classificazione, mentre la regressione lineare è un algoritmo regressore che restituisce come risposta un altro valore (non una classe) tramite l'interpolazione di dati. Per un approfondimento la differenza tra classificatori e regressori.
Il funzionamento
Nella fase di addestramento l'algoritmo di regressione logistica prende in input n esempi da un insieme di training (X).
Ogni singolo esempio è composto da m attributi e dalla classe corretta di appartenenza.
Durante l'addestramento l'algoritmo elabora una distribuzione di pesi (W) che permetta di classificare correttamente gli esempi con le classi corrette.
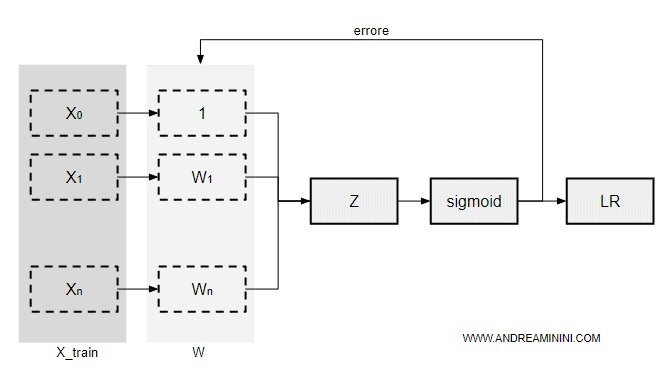
Poi calcola la combinazione lineare z del vettore dei pesi W e degli attributi xm
$$ z = \vec{x} \cdot \vec{w} + b $$
$$ z = x_0 \cdot w_0 + ... + x_m \cdot w_m + b$$
La combinazione lineare z viene passata alla funzione logistica (sigmoid) che calcola la probabilità di appartenenza del campione alle classi del modello.
$$ φ ( z ) = \frac{1}{1+e^{-z}} $$
La funzione sigmoid calcola la probabilità di appartenenza del campione alle classi.
E' la tipica curva a S della distribuzione delle probabilità.
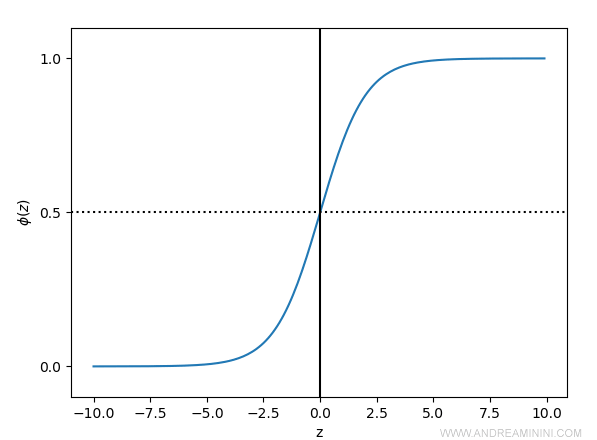
Nota. La funzione logistica è particolarmente utile perché gran parte dei fenomeni naturali segue l'andamento della curva logistica.
In pratica, la funzione sigmoid prende un valore reale z ottenuto con la combinazione lineare WT X = w0+w1x1 + ... + wnxn e lo trasforma in un numero compreso nell'intervallo [0,1].
Ad esempio
$$ φ ( z=2.5 ) = 0.8 $$
Questo valore indica la probabilità di appartenenza a una classe piuttosto che un'altra.
Nota. In alcuni casi non è utile conoscere se una combinazione di valori degli attributi x appartiene a una classe specifica, bensì conoscere la probabilità con cui appartiene alla classe. Da questo punto di vista la regressione logistica è molto utile.
A cosa serve la funzione logistica?
La funzione logistica è la funzione di attivazione nei nodi della rete neurale.
Il valore della funzione logistica viene convertito in un valore binario (1=attivo 0=non attivo) tramite una funzione di passo unitario (o quantizzatore).
Ad esempio, se il valore della funzione è maggiore di 0.5 il nodo viene attivato.
$$ \begin{cases} 1 \:\: se \:\: φ(z)>0.5 \\ \\ 0 \:\: altrimenti \end{cases} $$
A questo punto l'algoritmo deve trovare il vettore dei pesi W* e il valore b* in grado di minimizzare l'errore.
Questo ricorda quello che accade nella regressione lineare wx+b dove la combinazione w e b deve minimizzare lo scarto quadratico medio.
Nella regressione logistica, invece di minimizzare la perdita al quadrato, si massimizza la probabilità secondo la funzione statistica di verosimiglianza al modello.
$$ L_{w,b} = \prod_{i=1..N} φ ( z_{(i)} )^{y_i}(1-φ (z_{(i)}))^{1-y_i} $$
Dove è la probabilità dell'esempio di appartenere alla classe, considerando che il modello è composto da due sole classi: una classe positiva (es. si), una classe negativa (es. no).
Quindi, l'etichetta yi è compresa tra 0 (non appartiene alla classe positiva) e 1 (appartiene alla classe positiva).
- Se yi=1 allora Lw,b=φ(z(i)) perché il secondo termine (1-φ(z(i)))0 è uguale a 1.
- Se yi=0 allora Lw,b=(1-φ(z(i))) perché il primo termine φ(z(i))0 è uguale a 1.
Nota. Si usa l'operatore della produttoria anziché la sommatoria perché la probabilità di osservare N etichette in N esempi è il prodotto della probabilità di ogni singola osservazione. In questa formula si suppone che le probabilità siano indipendenti tra loro.
In alternativa, piuttosto che massimizzare la probabilità, posso massimizzare la verosimiglianza tramite la log-probabilità.
$$ L_{w,b} = \sum_{i=1}^N y_i \log φ(z_{(i)}) (x) + (1-y_i) \log (1-φ(z_{(i)})) $$
Essendo una sommatoria è più agevole da calcolare.
Il risultato è equivalente.
Un'altra alternativa utilizzabile come funzione di ottimizzazione consiste nel riscrivere la log-probabilità come una funzione di costo da minimizzare.
$$ J(w) = \sum_{i=1}^N - y_i \log φ(z_{(i)}) (x) - (1-y_i) \log (1-φ(z_{(i)})) $$
In questo modo se il modello risponde correttamente a un esempio, la sommatoria somma un costo pari a zero.
Viceversa, se risponde in modo errato somma un costo che tende a infinito.
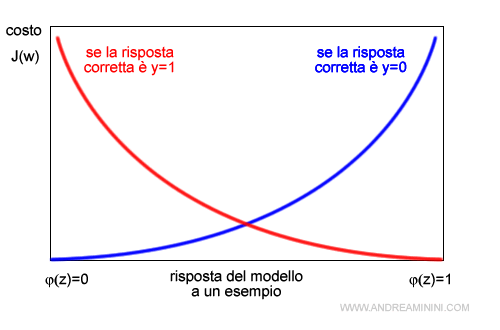
Ad esempio, se la risposta corretta di un esempio è y=1 (curva rossa) e il modello risponde correttamente φ(z)=1 all'esempio, il costo è zero.
Viceversa, se il modello risponde in modo errato φ(z)=0, il costo da aggiungere alla sommatoria è molto alto.
E così via.
