Algoritmo Version Space ( Spazio delle versioni )

Lo spazio delle versioni ( o version space ) è un sottoinsieme delle ipotesi consistenti in un processo di apprendimento induttivo incrementale ( concept learning ).

Chi l'ha inventato? Il primo algoritmo basato sull'idea dello spazio delle versioni è stato sviluppato da Tom M. Mitchell per ricercare una soluzione a un problema in un insieme completo delle ipotesi. L'algoritmo è anche detto algoritmo a eliminazione dei candidati.

Si basa sull'ordinamento delle ipotesi ( generality ordering ) in due gruppi estremi, quelle più generali e quelle più specifiche.

Come funziona l'algoritmo

Tutte le ipotesi consistenti h₁,...,h_n sono incluse nello spazio delle ipotesi H.

Lo spazio H è a sua volta composto da due sottoinsiemi GB e SB.

• Ipotesi consistenti più generali (GB). La regola di appartenenza all'insieme GB è più rilassata, ampia e/o comprende poche feature (attributi).
  
  Esempio
  
  Lo spazio delle ipotesi GB è un insieme composto da n ipotesi (H). Formalmente è una disgiunzione logica di n ipotesi H.
  

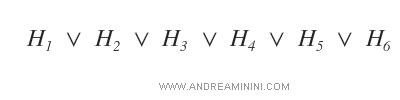
  Nota. Ogni ipotesi Hi è caratterizzata da un'espressione condizionale che deve essere vera per ogni istanza, ossia per ogni esempio dell'insieme di training. L'espressione condizionale è composta da operatori logici e attributi. Ad esempio ( x₁ ∧ x₂ ∧ x₃ ).

  
• Ipotesi consistenti più specifiche (SB). La regola di appartenenza all'insieme SB è più rigida, specifica e/o comprende molte feature (attributi).
  
  Esempio
  
  Lo spazio delle ipotesi SB è una disgiunzione di un minor numero di ipotesi, perché la regola di appartenenza è più restrittiva. L'insieme contiene meno ipotesi rispetto a GB.
  

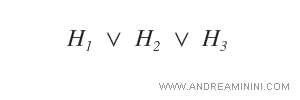
Cosa significa consistenti? Vuol dire che le ipotesi devono concordare con tutti i dati e gli esempi finora osservati nel processo di training.

I due insiemi GB e SB sono sottoinsiemi estremi e non compongono tutto lo spazio delle versioni H.

Lo spazio non incluso tra GB e SB è composto dalle ipotesi consistenti h più specifiche di GB e più generali di SB.

In pratica, ogni ipotesi al di fuori di GB e SB deve:

1. rifiutare tutti gli esempi rifiutare da GB perché è un'ipotesi più specifica rispetto a GB.
2. accettare tutti gli esempi accettati da SB perché è un'ipotesi più generale rispetto a SB

E' opportuno sottolineare che anche le ipotesi intermedie sono ipotesi consistenti.

Nota. Questo approccio mi consente di analizzare uno spazio delle ipotesi H anche teoricamente infinito. Mi basta definire due sottospazi estremi di ipotesi, uno più generale (GB) e un altro più specifico (SB). Tutto lo spazio intermedio non lo conosco ma so comunque che è composto da ipotesi consistenti ed è il campo di esplorazione delle possibili soluzioni del problema.

Durante il processo di apprendimento i nuovi esempi eliminano le ipotesi non più consistenti e modificano la frontiera dei sottospazi GB e SB, avvicinandole tra loro.

Nel corso del learning process lo spazio delle ipotesi consistenti diventa sempre più delimitato.

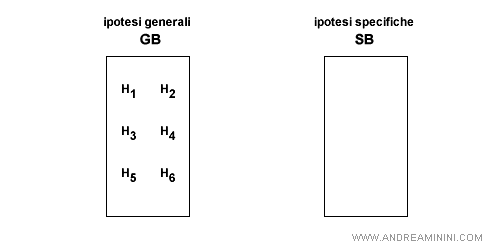
1] Fase iniziale

Nella fase iniziale tutte le ipotesi h di H sono incluse nell'insieme GB. Pertanto, inizialmente GB coincide con H.

L'insieme SB è invece un sottoinsieme vuoto.

2] Processo di apprendimento

Il processo di apprendimento verifica i primi esempi dell'insieme di training con tutte le n ipotesi.

• Falso positivo per SB. L'ipotesi S è troppo generica per l'esempio. Non essendo possibile specializzare ulteriormente l'ipotesi, perché uscirebbe dalla sinistra di SB, si elimina l'ipotesi da SB.
  
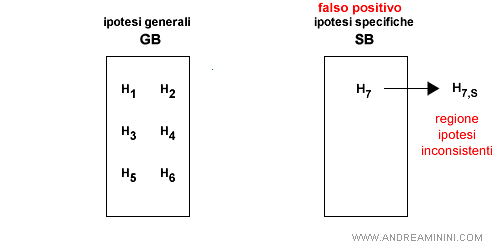
• Falso negativo per SB. L'ipotesi S è troppo specifica per l'esempio. E' possibile trasformare l'ipotesi S nelle sue generalizzazioni più vicine. E' però necessario che le generalizzazioni siano più specifiche di qualche elemento di GB.
  

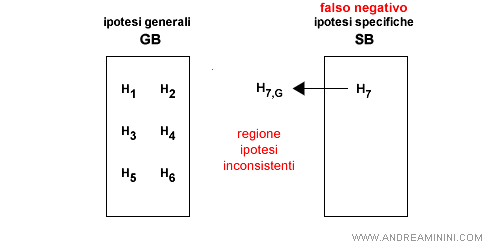
  Esempio. Un esempio di generalizzazione di un'ipotesi troppo specifica.
  

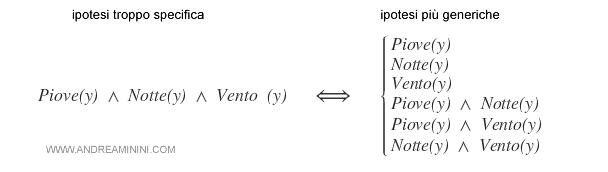
• Falso positivo per GB. L'ipotesi S è troppo generica per essere consistente con l'esempio. E' però possibile sostituirla con tutte le specializzazioni più vicine, purché siano più generiche di qualche elemento di SB.
  

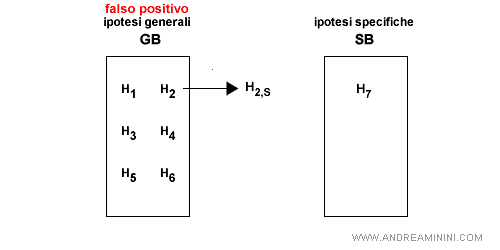
  Esempio. Un esempio pratico di specializzazione di un'ipotesi troppo generica.
  

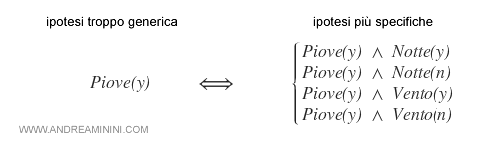
• Falso negativo per GB. L'ipotesi S è troppo specifica per l'esempio. Tuttavia, in questo caso non è possibile generalizzare ulteriormente l'ipotesi perché uscirebbe a sinistra di GB. Quindi, si può eliminare del tutto l'ipotesi S dallo spazio delle versioni.
  

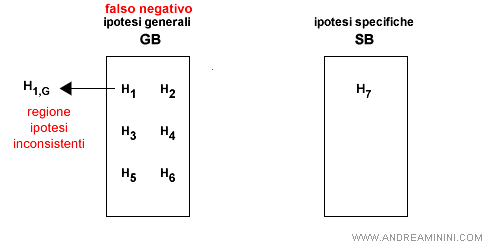
Nota. Un falso positivo si verifica quando la risposta dell'ipotesi è positiva ma quella dell'esempio è negativa. Un falso negativo si verifica quando la risposta dell'ipotesi è negativa ma quella dell'esempio è positiva.

Un esempio pratico

Ho un insieme di training composto da 5 esempi.

Ogni esempio è una congiunzione logica di 5 attributi (x₁,...,x₅) e un risultato (y) che identifica la risposta corretta.

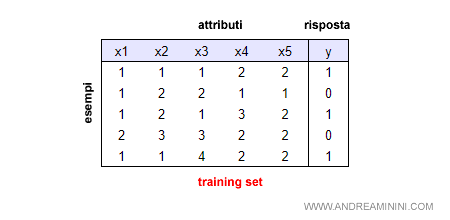
Nota. Un training set addestra la macchina a prendere una decisione corretta tramite degli esempi di addestramento. Pertanto, ogni training set risponde a una domanda specifica ( es. se la domanda è "giro a destra?", la risposta y può essere si (y=1) oppure no (y=0). E così via.

Per semplicità parto da uno spazio delle ipotesi composto da una sola ipotesi H₁.

H₁ = < 1, ? , ? , ? , ? >

Vuol dire che secondo l'ipotesi la risposta è y=1 (positiva) se l'attributo x₁ è uguale a uno (x₁=1). Il valore degli altri attributi è indifferente.

Inserisco questa ipotesi nell'insieme GB.

G₁ = < 1, ? , ? , ? , ? >

Lo spazio delle versioni iniziale è il seguente:

A questo punto posso cominciare ad analizzare gli esempi del training set.

Esempio 1

Secondo l'esempio 1 la risposta è y=1 se

E₁ = < 1, 1 , 1 , 2 , 2 > ⇒ y' = 1

Questo esempio è più specifico rispetto all'ipotesi generale G₁.

L'ipotesi G₁ è consistente con l'esempio perché l'attributo x₁ è uguale sia in H₁ che in E₁.

E₁ = < 1, 1 , 1 , 2 , 2 >
G₁ = < 1, ? , ? , ? , ? >

Quindi aggiungo l'esempio E₁ nell'insieme SB che inizialmente era vuoto.

S₁ = < 1, 1 , 1 , 2 , 2 >

Ora lo spazio delle versioni è il seguente:

Esempio 2

Secondo l'esempio 2 la risposta è y'=0 (negativa) se

E₂ = < 1, 2 , 2 , 1 , 1 > ⇒ y' = 0

Lo confronto con le ipotesi in GB e SB.

E₂ = < 1, 2 , 2 , 1 , 1 >
G₁ = < 1, ? , ? , ? , ? >
S₁ = < 1, 1 , 1 , 2 , 2 >

Si tratta di un falso negativo rispetto all'ipotesi G₁ perché restituisce y'=0 anche quando l'attributo x₁=1.

L'ipotesi G₁ non è consistente con l'esempio.

Cos'è un falso positivo? Un falso positivo si verifica quando l'ipotesi G₁ prevede un risultato positivo ( y=1 ) ma la risposta corretta dell'esempio di training E₂ è negativa ( y'=0 ).

Questo vuol dire che l'ipotesi G₁ è un'ipotesi troppo generica rispetto agli esempi E₁ e E₂.

Occorre rimpiazzare G₁ con le sue specializzazioni purché siano più generali rispetto a S₁.

G₂ = < ?, 1 , ? , ? , ? >
G₃ = < ?, ? , 1 , ? , ? >
G₄ = < ?, ? , ? , 2 , ? >
G₅ = < ?, ? , ? , ? , 2 >

Nota. Le precedenti ipotesi sono tutte le specializzazioni di G₁ consistenti e più generiche di S₁ dove S₁ è uguale < 1, 1 , 1 , 2 , 2 >.

Lo spazio delle versioni aggiornato è il seguente:

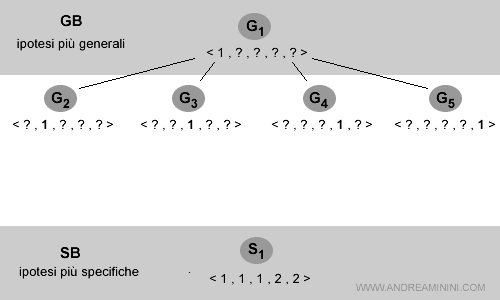
Esempio 3

Secondo l'esempio 3 la risposta è y'=1 (positiva) se

E₃ = < 1, 2 , 1 , 3 , 2 > ⇒ y' = 1

Lo confronto con le ipotesi in GB e SB.

E₃ = < 1, 2 , 1 , 3 , 2 >
G₂ = < ?, 1 , ? , ? , ? >
G₃ = < ?, ? , 1 , ? , ? >
G₄ = < ?, ? , ? , 2 , ? >
G₅ = < ?, ? , ? , ? , 2
S₁ = < 1, 1 , 1 , 2 , 2 >

Analizzando i nuovi dati, le ipotesi G₂ e G₄ non sono più consistenti con gli esempi E₁, E₂, E₃.

D'altra parte il nuovo esempio E₃ modifica anche l'ipotesi specifica S₁.

E₃ = < 1, 2 , 1 , 3 , 2 >
S₁ = < 1, 1 , 1 , 2 , 2 >
------------------------------
S₂ = < 1, ? , 1 , ? , 2 >

L'ipotesi S₂ è più generica rispetto a S₁ ed è consistente con tutti gli esempi.

Lo spazio delle versioni aggiornato è il seguente:

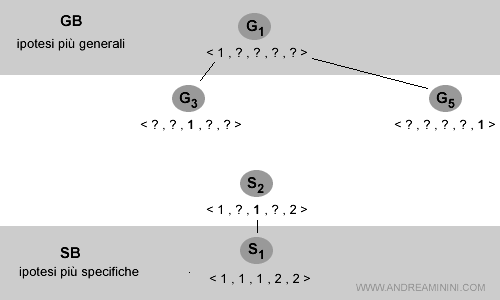
Esempio 4

Secondo l'esempio 4 la risposta è y'=0 (negativa) se

E₄ = < 2, 3 , 3 , 2 , 2 > ⇒ y' = 0

Confronto l'esempio con le ipotesi negli insiemi GB e SB.

E₄ = < 2, 3 , 3 , 2 , 2 > ⇒ y' = 0
G₃ = < ?, ? , 1 , ? , ? > ⇒ y = 1
G₅ = < ?, ? , ? , ? , 2 > ⇒ y = 1
S₂ = < 1, ? , 1 , ? , 2 > ⇒ y = 1

Le ipotesi G₃ e G₅ non sono consistenti perché troppo generiche.

Quindi, le sostituisco con le loro dirette specializzazioni che siano più generali rispetto alle ipotesi di SB.

G₃ = < ?, ? , 1 , ? , ? > ⇒ G₆ = < 1, ? , ? , ? , 2 >
G₅ = < ?, ? , ? , ? , 2 > ⇒ G₇ = < ?, ? , 1 , ? , ? >

Nota. Le precedenti ipotesi sono le specializzazioni di G₃ e G₅ consistenti e più generiche di S₂ dove S₂ è uguale < 1, ? , 1 , ? , 2 >.

Lo spazio delle versioni aggiornato è il seguente:

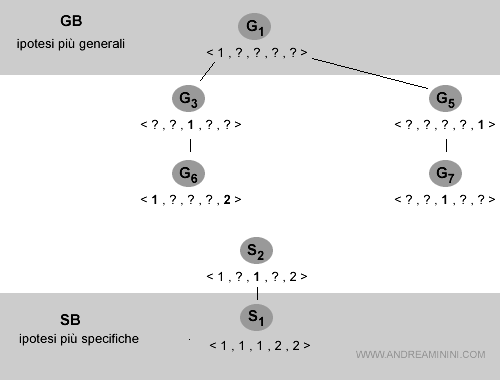
Esempio 5

Secondo l'esempio 5 la risposta è y'=1 (positiva) se

E₅ = < 1, 1 , 4 , 2 , 2 > ⇒ y' = 0

Confronto l'esempio con le ipotesi di GB e SB.

E₅ = < 1, 1 , 4 , 2 , 2 > ⇒ y' = 0
G₆ = < 1, ? , ? , ? , 2 > ⇒ y = 1
G₇ = < ?, ? , 1 , ? , ? > ⇒ y = 1
S₂ = < 1, ? , 1 , ? , 2 > ⇒ y = 1

L'ipotesi G₆ è consistente mentre l'ipotesi G₇ non è più consistente con tutti gli esempi.

Il nuovo esempio E₄ modifica anche l'ipotesi specifica S₂.

E₅ = < 1, 1 , 4 , 2 , 2 >
S₂ = < 1, ? , 1 , ? , 2 >
------------------------------
S₃ = < 1, ? , ? , ? , 2 >

L'ipotesi S₃ è più generica rispetto a S₂ ed è consistente con tutti gli esempi da E₁ a E₅.

Ora lo spazio delle versioni è il seguente:

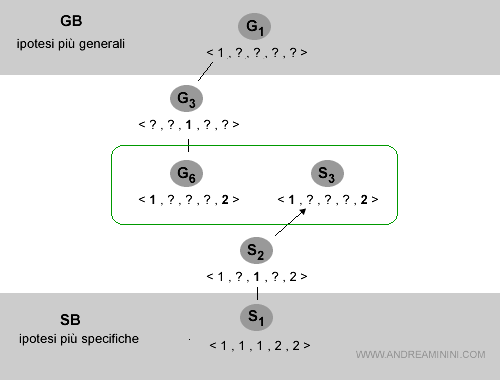
Gli esempi sono finiti e gli insiemi GB e LB coincidono.

G₆ = < 1, ? , ? , ? , 2 > ⇒ y = 1
S₃ = < 1, ? , ? , ? , 2 > ⇒ y = 1

L'algoritmo ha trovato l'ipotesi che giustifica una risposta positiva (y=1).

In questo modo, la macchina ha appreso una regola di comportamento tramite gli esempi ( training set ).

E se ci fosse più di un'ipotesi?

Con altri esempi gli insiemi GB e LB potrebbero anche non coincidere.

In questo caso, il risultato non sarebbe più una sola ipotesi ma la somma delle ipotesi contenute in GB e LB.

E se non esistesse nessuna ipotesi?

E' un altro risultato possibile dell'apprendimento.

Gli insiemi GB e LB potrebbero diventare insiemi vuoti alla fine del processo di apprendimento.

In questo caso, non ci sarebbero elementi per decidere e il processo di apprendimento fallisce.

Nota. Se gli insiemi GB e LB diventassero insiemi vuoti prima di aver analizzato tutti gli esempi, sarebbe del tutto inutile analizzare anche gli esempi restanti del training set. L'algoritmo termina l'esecuzione con un fallimento.

Lo pseudocodice dello spazio delle versioni

L'algoritmo prende in input il set di training degli esempi.

Inoltre, ha in memoria lo spazio delle versioni V ossia le ipotesi consistenti.

1. function SPAZIO VERSION ( esempi )
2. E = esempi ( set training in input )
3. V = insieme delle ipotesi ( spazio delle versioni )
4. for each esempio in E do
5. if V non è vuoto then V = { h in V : h consistente con esempio }
6. return V ( spazio delle versioni )

L'algoritmo analizza ogni esempio in E, dal primo all'ultimo, tramite la struttura iterativa compresa nelle righe 4 e 5.

Quando analizza un esempio, l'algoritmo aggiorna lo spazio delle versioni per rendere le ipotesi di V consistenti con l'esempio che sta analizzando ( riga 5 ).

Pertanto, lo spazio delle versioni tende a ridimensionarsi man mano che analizza nuovi esempi.

Al termine dell'iterazione l'algoritmo restituisce lo spazio delle versioni finale, quello consistente con tutti gli esempi ( riga 6 ).

Nota. Questo pseudocodice può essere implementato con qualsiasi linguaggio di programmazione.

Se lo spazio delle ipotesi V diventa un insieme vuoto, l'algoritmo cessa di aggiornarlo perché la ricerca è fallita.

In questo caso non ci sono ipotesi consistenti con tutti gli esempi di E.

Pro e contro dell'algoritmo

L'algoritmo Version Space ha i seguenti vantaggi:

• Non torna mai indietro. A differenza di altri algoritmi di apprendimento induttivo, lo spazio delle versioni non richiede il backtracking. E' un algoritmo incrementale.

I principali svantaggi sono i seguenti:

• Lo spazio delle ipotesi è enorme. Anche prendendo soltanto le due ipotesi estreme H_GB e H_SB, non si può essere sicuri che l'intervallo comprenda tutte le possibili ipotesi ossia tutte le risposte o le soluzioni di un problema.
• Se gli attributi nel training set sono pochi o c'è molto rumore nei dati, lo spazio delle ipotesi tende a collassare rapidamente.
• Se gli attributi nel training set sono tanti, lo spazio delle versioni GB⇔SB potrebbe crescere esponenzialmente con la specializzazione delle ipotesi.