Matrice di confusione

La matrice di confusione (confusion matrix) è uno strumento per analizzare gli errori compiuti da un modello di machine learning.

A cosa serve? E' utile per valutare la qualità delle previsioni del modello di classificazione. In particolar modo, la matrice mette in evidenza dove sbaglia il modello, in quali istanze risponde peggio e quali meglio.

Come costruire la matrice di confusione

Prendo il semplice caso di un classificatore binario.

Le classi sono due: SI o NO

Esempio. Un esempio di classificatore binario è il filtro antispam sulla posta in arrivo. Il modello deve decidere se l'email in entrata è spam oppure no.

Elenco le classi del problema nelle righe e nelle colonne.

• Nelle righe indico le classi effettive. Sono le classi delle risposte corrette.
• Nelle colonne indico le classi di previsione. Sono le classi delle risposte del modello.

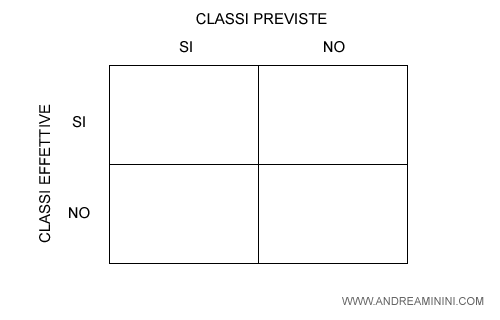
Nota. La matrice di confusione può essere costruita anche su più classi. Non solo su due. Ecco un esempio pratico di confusion matrix multiclasse con tre classi.

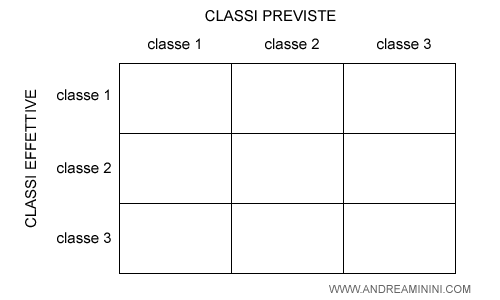
All'interno delle caselle inserisco le risposte del modello alle varie istanze.

Ad esempio, il modello analizza 80 email e le classifica spam/no spam. In 60 casi il modello classifica correttamente mentre in 20 sbaglia.

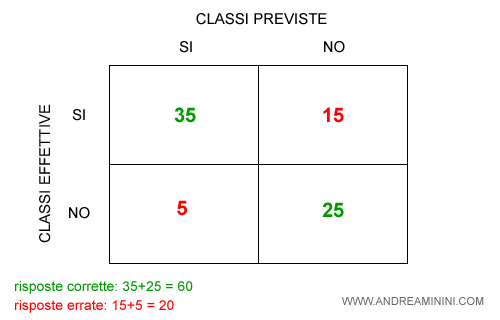
Gli errori e le risposte corrette però non sono tutte uguali.

Possono verificarsi quattro casi:

• True positive (TP)
  Se la classe prevista è SI ed è uguale alla classe effettiva, si tratta di un caso di true positive (vero positivo). Il modello ha risposto correttamente SI.
• True negative (TN)
  Se la classe prevista è NO ed è uguale alla classe effettiva, si tratta di un caso di true negative (vero negativo). Il modello ha risposto correttamente NO.
• False positive (FP)
  Se la classe prevista è SI ma è diversa dalla classe effettiva, si tratta di un caso di false positive (falso positivo). Il modello ha sbagliato a rispondere SI.
• False negative (FN)
  Se la classe prevista è NO ma è diversa dalla classe effettiva, si tratta di un caso di false negative (falso negativo). Il modello ha sbagliato a rispondere NO.

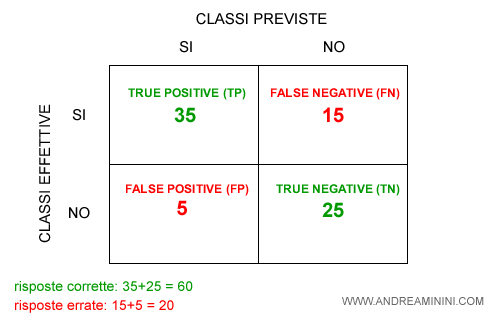
La matrice di confusione rende più facile l'analisi degli errori.

Esempio. Nella matrice di confusione precedente è subito evidente che il modello lascia passare email di spam (false negative). Circa 15 email di spam sono ritenute valide. Sono invece meno frequenti i falsi positivi, soltanto 5 email valide ritenute erroneamente spam. Per approfondire la differenza tra falsi positivi e falsi negativi.

Le metriche della matrice di confusione

Dalla matrice di confusione posso ottenere facilmente diverse metriche:

• Il tasso di errore
  Il tasso di errore (error rate) misura la percentuale di errore delle previsione sul totale delle istanze. Varia da 0 (migliore) a 1 (peggiore). $$ ERR = \frac{FP+FN}{TP+TN+FP+FN} $$

  

• L'accuratezza
  L'accuratezza (accuracy) misura la percentuale delle previsioni esatte sul totale delle istanze. E' l'inverso del tasso di errore. Varia da 0 (peggiore) a 1 (migliore). $$ ACC = \frac{TP+TN}{TP+TN+FP+FN} = 1-ERR $$

  

• La precisione
  La precisione (precision) è la percentuale delle previsioni positive corrette (TP) sul totale delle previsioni positive del modello (giuste TP o sbagliate FP). $$ PR = \frac{TP}{TP+FP} $$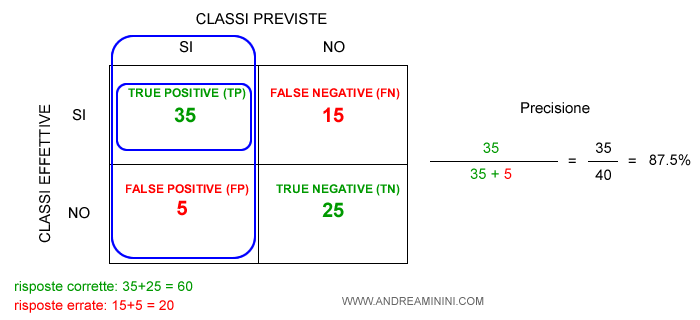

  

• Il richiamo o sensitività
  Il richiamo (o recall) o sensitività (sensitivity) è la percentuale delle previsioni positive corrette (TP) sul totale delle istanze positive. Varia da 0 (peggiore) a 1 (migliore). $$ Recall = \frac{TP}{TP+FN} $$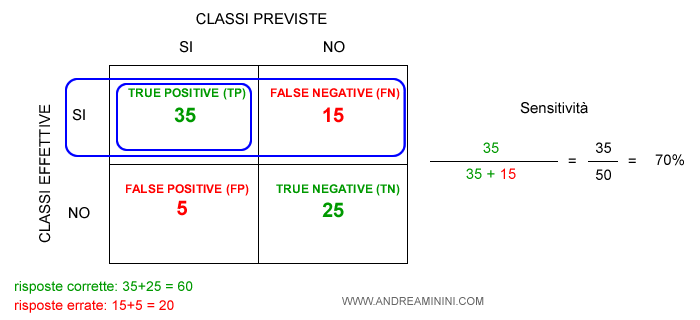

  

• La specificità
  La specificità (specificity) è la percentuale delle previsioni negative corrette (TN) sul totale delle istanze negative. Varia da 0 (peggiore) a 1 (migliore). $$ SP = \frac{TN}{TN+FP} $$

  

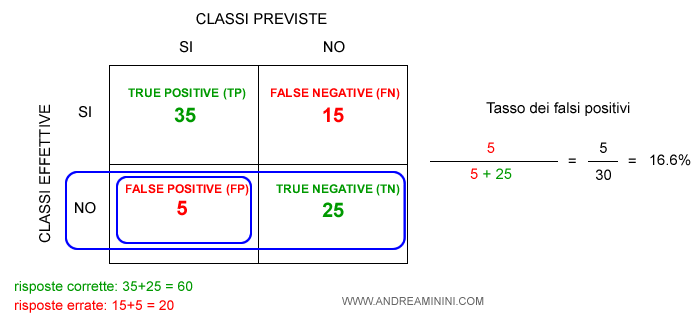
• Il tasso dei falsi positivi

  Il tasso dei falsi positivi (False Positive Rate) è la percentuale delle previsioni positive errate (FP) sul totale delle istanze negative. Varia da 0 (migliore) a 1 (peggiore). $$ FPR = \frac{FP}{TN+FP} $$

  

• Punteggio F
  Il punteggio F (F-Score) è la media armonica delle metriche Precision e Recall. Varia da 0 (peggiore) a 1 (migliore). $$ FS = \frac{2 \cdot Recall \cdot Precision }{Recall + Precision} $$

  $$ FS = \frac{2 \cdot 0.70 \cdot 0.875 }{0.70 + 0.875} = \frac{1.225 }{1.575} = 0.77 $$

E così via.