Divisione in algebra relazionale

La divisione è un operatore binario dell'algebra relazionale che contiene le tuple <x> della prima relazione A tali che per ogni tupla <y> della seconda relazione B ci sia una tupla <x,y> nella prima relazione A. $$ A/B = \{ <x> \: | \: \forall <y> \in B, <x,y> \in A \} $$

Si tratta di un operatore derivato perché si ottiene combinando altri operatori primitivi dell'algebra relazionale.

A/B = ∏_x(A) - N

Dove N sono i valori interdetti di A ossia quei valori <x> di A che associati a <y> di B formano una tupla <x,y> non presente in A.

N = ∏_x((∏_x(A) x B)-A)

Un esempio pratico

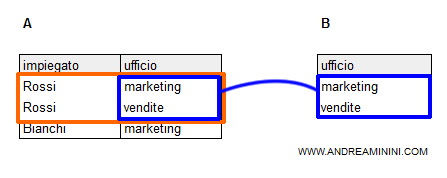
Ho una relazione A di impiegati e una relazione B degli uffici di un'azienda

Per trovare gli impiegati che lavorano in tutti i reparti si ricorre alla divisione A/B.

A/B

Nella tabella A c'è solo un valore <impiegato> tale che ogni <impiegato,ufficio> è compreso in A.

Il risultato è una tabella contenente l'impiegato che lavora in entrambi i reparti.

In questo caso è l'impiegato Rossi.

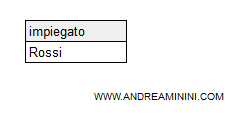
Nota. Nella tabella della divisione è escluso l'attributo in comune "ufficio".

E così via.