Prodotto cartesiano in algebra relazionale
Il prodotto cartesiano è un operatore binario insiemistico dell'algebra relazionale che, date due relazioni r1 e r2, crea una relazione composta da tutte le combinazioni possibili delle tuple della prima con le tuple della seconda. Il simbolo del prodotto cartesiano è x. $$ r_3 = r_1 \: x \: r_2 $$
Nel prodotto cartesiano ogni tupla della prima relazione è seguita da tutte le tuple della seconda relazione.
E' un operatore insiemistico perché ha lo stesso significato matematico del prodotto cartesiano nella teoria degli insiemi.
Nota. Nel caso del prodotto cartesiano non è necessario che le tuple siano omogenee. Pertanto, non è richiesta la compatibilità rispetto all'unione.
Un esempio pratico
Ho due tabelle S e T.
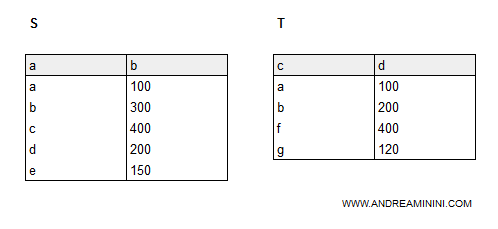
Calcolo il prodotto cartesiano delle due tabelle.
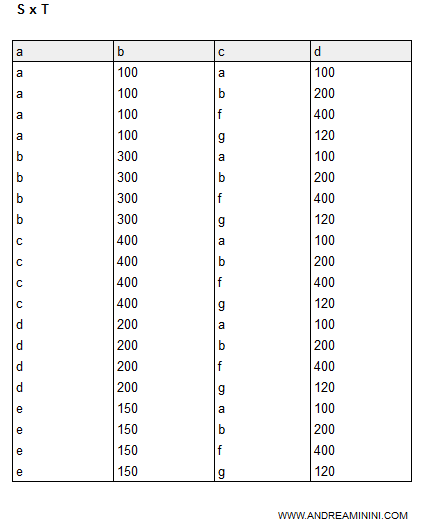
S x T
Il prodotto cartesiano è una tabella (relazione) composta da tutte le tuple della prima relazione combinate con tutte le relazioni della seconda.
Il conflitto di nomi negli attributi
Se le relazioni r1 e r2 hanno degli attributi con lo stesso nome, per convenzione nel prodotto cartesiano i campi corrispondenti sono indicati senza alcun nome.
Esempio
Queste due tabelle hanno un attributo con lo stesso nome (b)

Come risolvere il conflitto di nomi?
Ci sono due soluzioni.
- Posso riconoscere gli attributi di origine in base alla loro posizione nello schema del prodotto cartesiano e ridenominarli (ex post).
- Posso ridenominare gli attributi con lo stesso nome nello schema delle tabelle di origine prima del prodotto cartesiano (ex ante).
Nota. In alcuni calcolatori di algebra relazionale gli attributi delle tabelle sono associati automaticamente a un prefisso uguale al nome della relazione di origine seguito da un punto di separazione. $$ NomeTabella \: . \: NomeAttributo $$ In questi casi il conflitto di nomi non può verificarsi.

E così via.
