Unione in algebra relazionale
L'unione è un operatore insiemistico binario dell'algebra relazionale che unisce due relazioni r1 e r2 (tabelle) in un'unica relazione r3. Il simbolo dell'unione è ∪. $$ r_3 = r_1 ∪ r_2 $$
Le due relazioni operandi r1 e r2 devono avere lo stesso numero e tipo (dominio) di attributi da sinistra verso destra, ossia tuple omogenee.
Il risultato è una relazione unione r3 composta da tutte le tuple delle due relazioni, senza duplicazioni.
La compatibilità non si verifica con i nomi degli attributi. Nell'unione le relazioni possono anche avere nomi di attributi diversi. In questo caso, l'unione eredita per convenzione i nomi degli attributi della prima relazione. E questo può creare problemi semantici legati al significato dell'informazione. Ad esempio, l'unione delle colonne denominate "padre" e "madre" (in due relazioni diverse) è una colonna "padre" anche se contiene entrambi i genitori.
Se una tupla è presente con gli stessi valori in entrambe le relazioni r1 e r2, viene considerata una sola volta nella tabella r3.
Pertanto, il numero delle tuple della relazione unione può essere uguale o inferiore alla somma delle tuple nelle relazioni operandi.
Un esempio pratico
Ho due relazioni S e T con lo stesso numero di attributi e stessi domini.
La prima relazione S ha 5 tuple mentre la seconda relazione T ha 4 tuple.
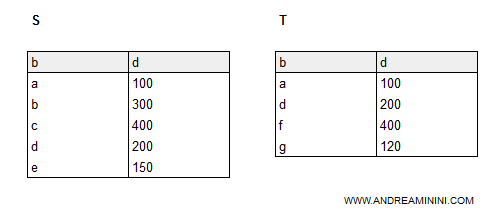
L'unione è una relazione composta da tutte le tuple delle due relazioni.
La relazione unione è composta da 7 tuple.
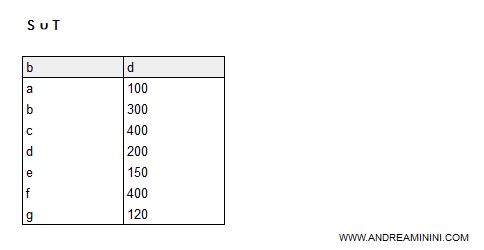
Perché la relazione di unione ha 7 tuple e non 9? Le tuple [a,100] e [d,200] sono presenti sia in S e sia in T. Pertanto, nell'unione S∪T le tuple [a,100] e [d,200] sono considerate una sola volta. Per questa ragione la relazione di unione ha 7 tuple anziché 9.
E così via.
