Intersezione in algebra relazionale
L'intersezione è un operatore insiemistico binario dell'algebra relazionale che seleziona le tuple in comune in due relazioni r1 e r2 (tabelle). Il simbolo dell'intersezione è ⋂. $$ r_3 = r_1 ⋂ r_2 $$
Le due relazioni operandi r1 e r2 hanno tuple omogenee, ossia lo stesso numero e tipo (dominio) di attributi visti da sinistra verso destra.
Il risultato dell'intersezione è una relazione composta dalle tuple presenti in entrambe le relazioni, senza duplicazioni.
La compatibilità non è sui nomi degli attributi. Nell'intersezione le relazioni possono anche avere nomi di attributi diversi. E' necessario però che il numero degli attributi e il dominio sia lo stesso. Se i nomi delle colonne sono diversi, per convenzione l'intersezione utilizza i nomi degli attributi della prima relazione (r1).
Quando una tupla con gli stessi valori è presente in entrambe le relazioni r1 e r2, è considerata una sola volta nella tabella intersezione r3.
E' un operatore insiemistico dell'algebra relazionale perché ha lo stesso significato dell'intersezione nella teoria degli insiemi.
Un esempio pratico
In questo esempio ho due relazioni S e T che hanno lo stesso numero di attributi e gli stessi domini.
La relazione S ha 5 tuple mentre la relazione T ha 4 tuple.
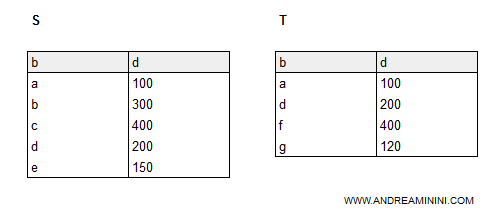
Nota. Le tuple delle relazioni S e T sono omogenee perché il numero degli attributi e il dominio è lo stesso visti da sinistra verso destra. Il nome delle colonne è casualmente lo stesso ma non è importante. I nomi delle colonne potevano anche essere diversi.
L'intersezione è una relazione composta dalle tuple presenti in entrambe le due relazioni prese una sola volta.
In questo caso la relazione di intersezione è composta da 2 tuple.

Le tuple [a,100] e [d,200] sono presenti sia in S e sia in T.
E così via.
