Selezione in algebra relazionale
La selezione è un operatore unario ortogonale dell'algebra relazionale che seleziona le tuple di una relazione (tabella) che soddisfano una particolare condizione. Il simbolo della selezione è sigma σ o SEL $$ σ_{ condizione} (relazione) $$ oppure $$ SEL_{condizione} (relazione) $$
Il risultato della selezione è una tabella con lo stesso schema della relazione r(X) in ingresso. Dove X è l'insieme degli attributi.
La selezione si dice operatore "ortogonale" perché seleziona le righe della tabella che soddisfano la condizione specificata, senza duplicazioni, mantenendo gli stessi attributi (X).
Pertanto, la selezione decompone la relazione orizzontalmente.
Nota. Un altro operatore ortogonale dell'algebra relazionale è la proiezione che, invece, seleziona le colonne di una tabella e decompone verticalmente la relazione. La proiezione e la selezione sono operazioni complementari tra loro.
La condizione di selezione è un'espressione booleana composta da operatori di confronto (>,<,=,>=,<=, <>) , attributi della relazione, costanti e connettivi logici ∨ (or), ∧ (and) e ¬ (not).
Un esempio pratico
Ho una generica tabella S composta da 5 tuple e 2 attributi b e d.
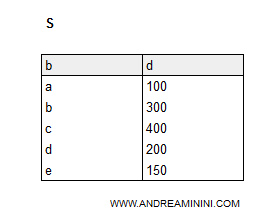
Seleziono le tuple con valore d>200
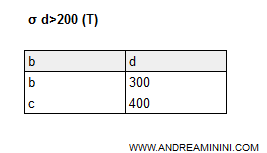
σd>200 (S)
Il risultato è una tabella composta soltanto dalle tuple in cui la condizione booleana d>200 è vera.
Soltanto 2 tuple [b,300] e [d,400] soddisfano la condizione di selezione.
Esempio 2
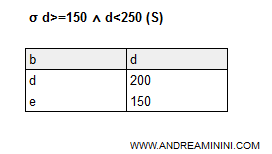
Ora seleziono tutte le tuple con l'attributo d compreso tra 150 (compreso) e 250 (escluso).
σd>=150∧d<250 (S)
In questo caso la condizione booleana include il connettivo and (∧).
Il risultato è una tabella composta dalle tuple [e,150] e [d,200].
E così via.
