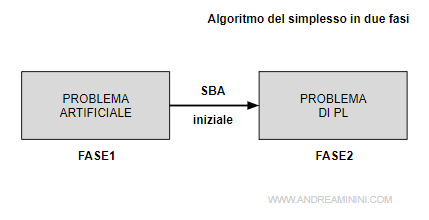
L'algoritmo del simplesso in due fasi

Cos'è l'algoritmo del simplesso in due fasi

L'algoritmo del simplesso in due fasi è suddiviso in due:

• Nella prima fase elaboro l'algoritmo su un problema artificiale per individuare una base ammissibile (se esiste). Possono verificarsi due casi:
  1. Il problema ammette soluzioni. Se la soluzione ottima del problema artificiale ha valore nullo (z=0), il problema originale ammette una soluzione. Passo alla fase 2.
  2. Il problema è inammissibile. Se la soluzione ottima del problema artificiale non ha valore nullo (z≠0), il problema originale non ammette soluzioni. Quindi non passo alla fase 2. L'algoritmo termina qui.
• Nella seconda fase elaboro l'algoritmo del simplesso sul problema costruito in forma canonica sulla base individuata nella prima fase.

La seconda fase (simplesso) viene eseguita soltanto se la prima fase è soddisfatta, ossia se il problema artificiale ha una soluzione.

A cosa serve

Uno dei problemi dell'algoritmo del simplesso è la scelta delle basi iniziali per costruire la forma canonica, ossia l'inizializzazione della SBA (Soluzione di Base Ammissibile).

Dalla scelta delle variabili di base iniziali dipende il numero di passaggi necessari per giungere alla risoluzione finale del problema (ottimo, illimitato, inammissibile).

L'algoritmo del simplesso in due fasi usa un algoritmo specifico per individuare la SBA iniziale migliore. Quindi, riduce il numero complessivo dei cicli di elaborazione.

Come funziona

Nella prima fase creo un problema artificiale PA a partire dal problema originale P in forma standard.

Introduco nel problema tante variabili artificiali quanti sono i vincoli del problema. Ogni variabile artificiale ha coefficiente unitario.

Nota. Nei vincoli dove ci sono già variabili ausiliarie con coefficiente unitario, quelle inserite per standardizzare la disequazione, non è necessario aggiungere un'altra variabile artificiale. In questo modo riduco l'onere computazionale del problema artificiale.

Sostituisco la funzione obiettivo con la somma delle variabili artificiali.

Faccio entrare le variabili artificiali nella base con delle operazioni pivot. In questo modo ottengo il problema artificiale in forma canonica sulla base composta dalle variabili artificiali.

Infine, cerco la soluzione ottimale del problema.

Una volta risolto il problema artificiale verifico il criterio di ammissibilità

• Se nella soluzione ottimale il valore ottimo della funzione obiettivo nel problema artificiale PA è nullo, allora il problema originale P è ammissibile. Si tratta di una condizione necessaria e sufficiente.
• Se nella soluzione ottimale il valore ottimo della funzione obiettivo nel problema artificiale PA non è nullo, il problema P è inammissibile e l'analisi termina qui. Non c'è bisogno di elaborare la seconda fase dell'algoritmo.

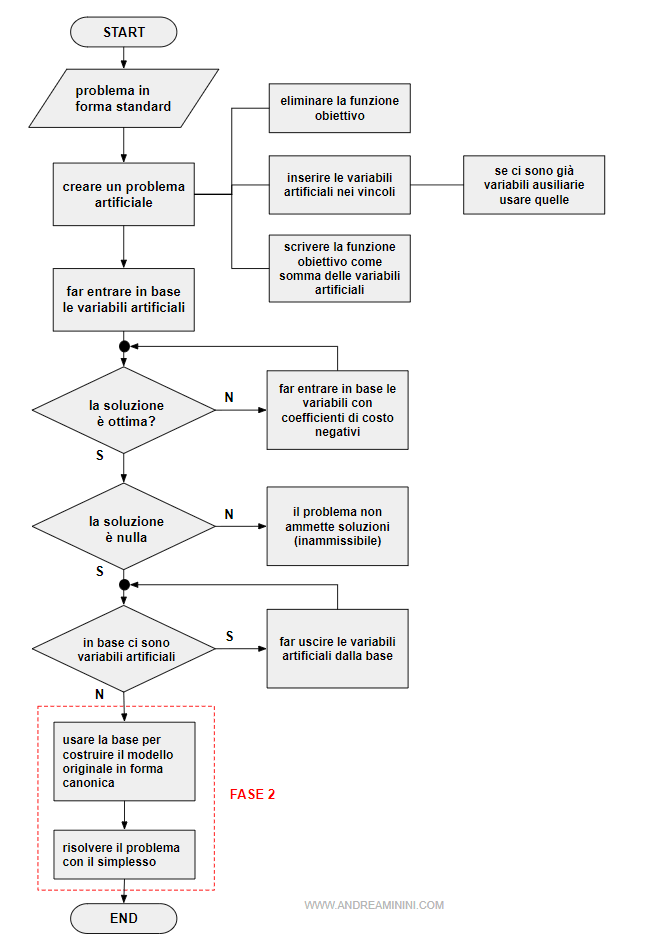
Ecco il processo sintetizzato in un diagramma di flusso.

Un esempio pratico

Ho il seguente problema

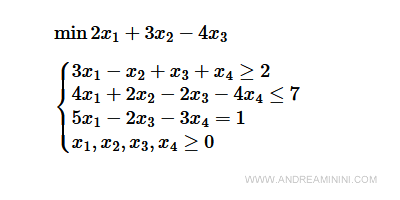
Lo trasformo in forma standard aggiungendo le variabili x5 e x6 alle prime due disequazioni

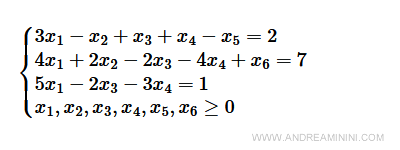
La matrice dei coefficienti A è

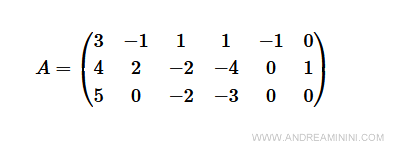
Nella matrice c'è già una colonna [0 1 0]^T quindi per realizzare una matrice identità mi basta aggiungere solo due variabili artificiali y₇ e y₈ nella prima e nell'ultima disequazione.

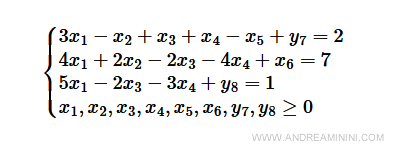
Ora la matrice dei coefficienti è

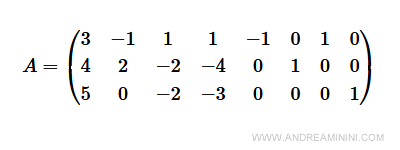
Le ultime tre colonne formano una matrice identità. Sono relative alle variabili x₆, y₇ e y₈

Posso formare la base iniziale B=(6,7,8) con tre operazioni pivot.

Prima di tutto sostituisco la funzione obiettivo del problema originale con la minimizzazione delle due variabili artificiali y₇+y₈

In questo modo ottengo il modello del problema artificiale

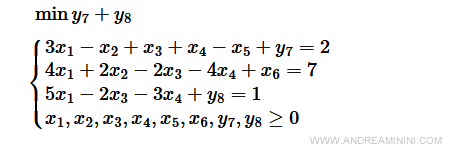
Poi calcolo la matrice pivot

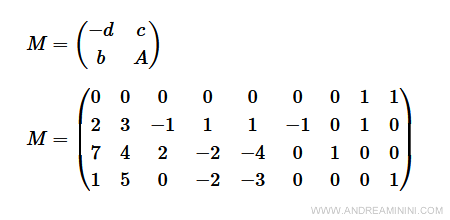
Infine svolgo le tre operazioni pivot per far entrare le variabili nella base.

Prima operazione pivot

Faccio entrare in base la variabile y₇ (k=7) che è definita nella prima equazione (h=1)

Quindi, la prima operazione pivot è (h,k)=(1,7).

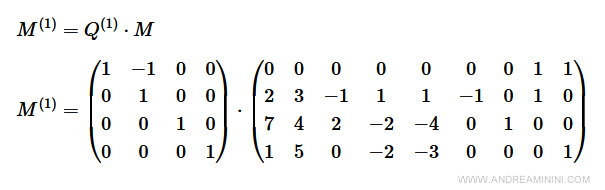
Spiegazione. La prima colonna e riga delle matrici M e Q è con indice zero (0). Sostituisco la colonna h=3 di Q (la quarta) con la colonna k=7 di M (l'ottava). Ogni elemento della colonna è moltiplicato per -1 e diviso per l'elemento pivot a_1,1=1 ad eccezione dell'elemento pivot stesso che è pari al suo inverso 1/a_1,1. Per un ulteriore spiegazione rimando agli appunti sull'operazione pivot.

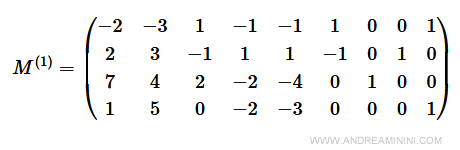
Seconda operazione pivot

Faccio entrare in base la variabile y₈ (k=8) che è definita nella terza equazione (h=3)

Quindi, la seconda operazione pivot è (h,k)=(3,8).

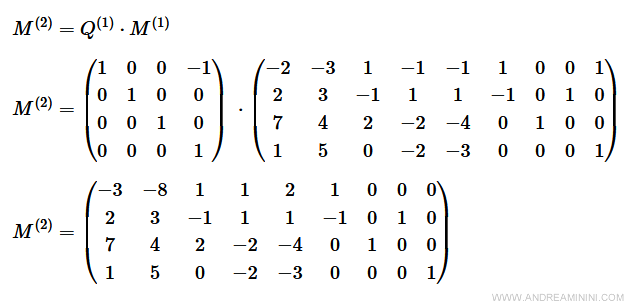
Terza operazione pivot

Faccio entrare in base la variabile x₆ (k=6) che è definita nella seconda equazione (h=2)

Quindi, la terza operazione pivot è (h,k)=(2,6).

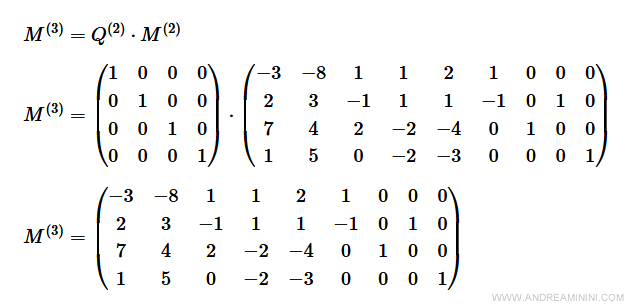
Sapendo che

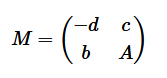
posso ricostruire il problema artificiale in forma canonica nella base iniziale B=[7,6,8]

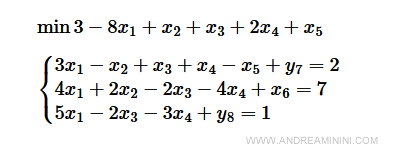
A] La fase 1 del simplesso

Una volta costruito il problema artificiale nella base iniziale, cerco di trovare la soluzione ottimale del problema.

In questo caso z=3 non è la soluzione ottimale, perché il coefficiente di costo -8 di x₁ è negativo e almeno un coefficiente tecnico è positivo.

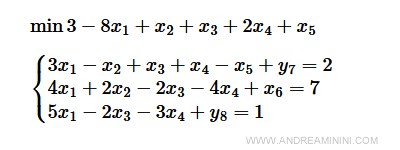
Pertanto, con un'ulteriore operazione pivot faccio entrare la variabile x₁ nella base B=[7,6,8] ossia k=1.

Per trovare la variabile uscente dalla base calcolo il minimo rapporto b/a nella colonna k=1 della matrice dei coefficienti quando a è positivo.

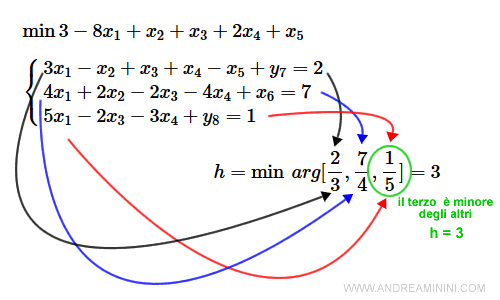
Quindi, la variabile uscente è relativa alla h=3 equazione del sistema ossia y₈.

Per fare il cambio di base calcolo l'operazione pivot (h,k)=(3,1)

L'elemento pivot nella matrice pivot M è (3,1) ossia a₃₁=5

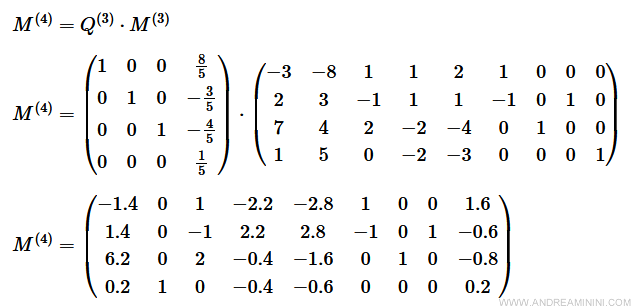
Ottengo il modello in forma canonica nella base B = [7,6,1].

Una variabile artificiale è uscita dalla base.

Sapendo che

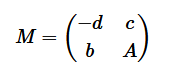
posso ricostruire il problema artificiale in forma canonica nella base iniziale B=[7,6,1]

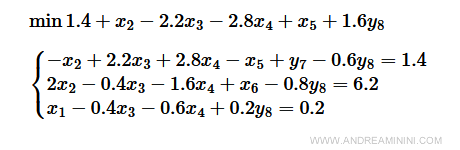
La soluzione z=1.4 non è la soluzione ottimale, perché i coefficienti di costo di x₃ e x₄ sono negativi e hanno almeno un coefficiente tecnico positivo.

Scelgo di far entrare in base x₄ perché ha il coefficiente di costo negativo più basso.

Con un'ulteriore operazione pivot faccio entrare la variabile x₄ nella base B=[7,6,1] ossia k=4.

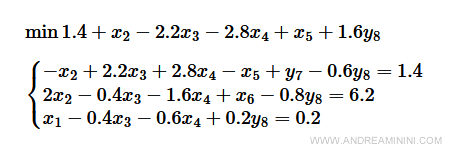
Per trovare la variabile uscente dalla base calcolo il minimo rapporto b/a nella colonna k=1 della matrice dei coefficienti quando a è positivo.

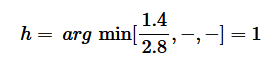
Quindi, la variabile uscente è relativa alla h=1 equazione del sistema ossia y₇.

Per fare il cambio di base calcolo l'operazione pivot (h,k)=(1,4)

L'elemento pivot nella matrice pivot M è (1,4) ossia a₁₄=2.8

Sapendo che

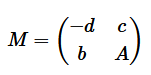
posso ricostruire il problema artificiale in forma canonica nella base iniziale B=[4,6,1]

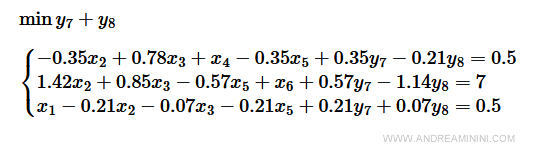
Quest'ultima soluzione z=0 è ottimale perché nessun coefficiente di costo è negativo.

La soluzione del problema artificiale è

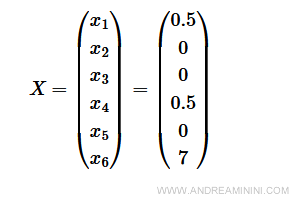
La soluzione del problema artificiale è un valore nullo z=0.

Pertanto, il problema originale è ammissibile e posso passare alla fase 2 dell'algoritmo del simplesso.

B] La fase 2 del simplesso

Il problema artificiale ha una soluzione ammissibile ottimale.

Pertanto, torno ad analizzare il problema originale.

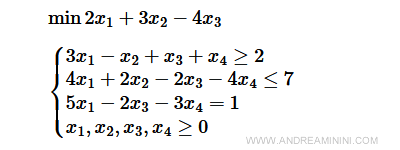
Il problema originale ha solo le variabili x₁, x₂, x₃, x₄

Quindi, posso ignorare le altre variabili del problema artificiale x₅ e x₆.

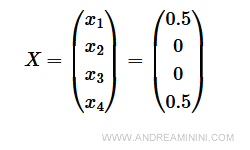
Quest'ultima soluzione è ammissibile anche per il problema originale.

Basta sostituire x₁=0.5 e x₄=0.5 nel problema originale mettendo a zero x₂=0 e x₃=0 per rendersene conto.

Ora trasformo il modello in forma standard.

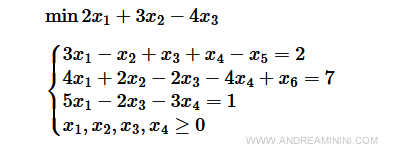
Poi lo trasformo in forma canonica rispetto alla base B=[4,6,1] trovata nel problema artificiale.

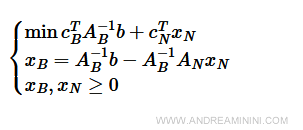
Calcolo la matrice inversa dei coefficienti di base

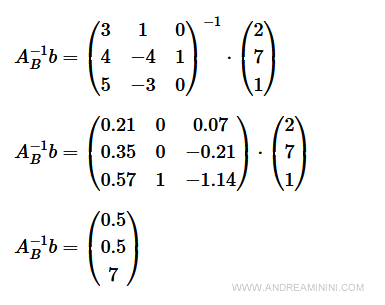
Quindi, le soluzioni sono ammissibili

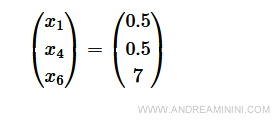
Svolgo i calcolo della forma canonica

In questo modo ottengo il problema in forma canonica nella base B=[4,6,1] trovata con il problema artificiale.

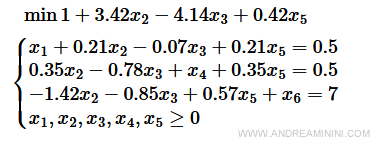
Le soluzioni sono le stesse.

Nota. In questo caso, senza ulteriori cambi di base, posso affermare che il problema è illimitato inferiormente perché il coefficiente di costo di x₃ è negativo e tutti i coefficienti tecnici di x₃ non sono positivi.

Esempio 2

Ho il seguente problema.

$$ \min 4x_1 - 2x_2 + 5_x3 \\ \begin{cases} 4x_1 - x_2 + 2x_3 + x_4 =6 \\ x_1 + 2x_2 - x_3 -2x_4 = 3 \\ -2x_1 + x_2 + 2x_3 = 4 \\ x_1, x_2, x_3,x_4 \ge 0 \end{cases} $$

Essendoci solo equazioni, il problema è già in forma standard.

FASE 1

Introduco tre variabili ausiliarie y₅, y₆, y₇ con coefficiente unitario. Una per ogni equazione.

$$ \min 4x_1 - 2x_2 + 5_x3 \\ \begin{cases} 4x_1 - x_2 + 2x_3 + x_4 + y_5 =6 \\ x_1 + 2x_2 - x_3- 2x_4 + y_6 = 3 \\ -2x_1 + x_2 + 2x_3 + y_7 = 4 \\ x_1, x_2, x_3,x_4 \ge 0 \end{cases} $$

Poi sostituisco la funzione obiettivo con la minimizzazione delle variabili ausiliarie.

$$ {\color{red} {\min y_5 + y_6 + y_7} } \\ \begin{cases} 4x_1 - x_2 + 2x_3 + x_4 + y_5 =6 \\ x_1 + 2x_2 - x_3- 2x_4 + y_6 = 3 \\ -2x_1 + x_2 + 2x_3 + y_7 = 4 \\ x_1, x_2, x_3,x_4 \ge 0 \end{cases} $$

Ora trasformo il problema in forma canonica facendo entrare in base le variabili ausiliarie y5, y6, y7 con tre operazioni pivot (1,5), (2,6), (3,7).

Prima di procedere calcolo la matrice pivot del problema

$$ M = \begin{pmatrix} -d & c \\ b & A \end{pmatrix} $$

$$ M = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 6 & 4 & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

Nota. Nella matrice pivot la prima riga e la prima colonna hanno indice zero. Non uno.

Poi procedo con le tre operazioni pivot.

Operazione pivot (1,5)

Con l'operazione pivot (h,k)=(1,5) faccio entrare in base la variabile y₅ (k=5) nella prima equazione (h=1).

$$ M^{(1)} = Q \cdot M $$

$$ M^{(1)} = \begin{pmatrix} 1 & -1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 6 & 4 & -1 & 2 & 1 & <1> & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

L'elemento pivot della matrice M è a_1,5=1. Per semplicità lo evidenzio con il simbolo < >.

Spiegazione. La matrice identità Q ha lo stesso numero di righe della matrice M. Anche Q ha la prima riga e colonna con indice zero. Sostituisco la colonna h=1 di Q (la seconda) con la colonna k=5 (la sesta) di M trasformata dopo l'operazione pivot. Per ulteriori informazioni rimando agli appunti sull'operazione pivot.

$$ M^{(1)} = \begin{pmatrix} -6 & -4 & 1 & -2 & -1 & 0 & 1 & 1 \\ 6 & 4 & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

Ora la base del problema è B(y₅ , _ , _ ).

Operazione pivot (2,6)

Con l'operazione pivot (h,k)=(2,6) faccio entrare in base la variabile y₆ (k=6) nella seconda equazione (h=2).

$$ M^{(2)} = Q^{(2)} \cdot M^{(1)} $$

$$ M^{(2)} = \begin{pmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} -6 & -4 & 1 & -2 & -1 & 0 & 1 & 1 \\ 6 & 4 & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & < 1> & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

L'elemento pivot della matrice M⁽¹⁾ è a_2,6=1.

$$ M^{(2)} = \begin{pmatrix} -9 & -5 & -1 & -1 & 1 & 0 & 0 & 1 \\ 6 & 4 & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

Ora la base del problema è B(y₅ ,y₆ , _ ).

Operazione pivot (3,7)

Con l'operazione pivot (h,k)=(3,7) faccio entrare in base la variabile y₇ (k=7) nella terza equazione (h=3).

$$ M^{(3)} = Q^{(3)} \cdot M^{(2)} $$

$$ M^{(3)} = \begin{pmatrix} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} -9 & -5 & -1 & -1 & 1 & 0 & 0 & 1 \\ 6 & 4 & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & <1 > \\\end{pmatrix} $$

L'elemento pivot della matrice M⁽²⁾ è a_3,7=1.

$$ M^{(3)} = \begin{pmatrix} -13 & -3 & -2 & -3 & 1 & 0 & 0 & 0 \\ 6 & 4 & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

Ora la base del problema è B(y₅ ,y₆ , y₇).

Ho ottenuto il problema artificiale in forma canonica rispetto alla base B(y₅ ,y₆ , y₇).

$$ \min 13 - 3x_1 - 2 x_2 - 3x_3 + x_4 \\ \begin{cases} 4x_1 - x_2 + 2x_3 + x_4 + y_5 =6 \\ x_1 + 2x_2 - x_3 2x_4 + y_6 = 3 \\ -2x_1 + x_2 + 2x_3 + y_7 = 4 \\ x_1, x_2, x_3,x_4 \ge 0 \end{cases} $$

La soluzione non è ottima perché ci sono coefficienti di costo negativi.

Inoltre, la base è composta da variabili ausiliarie.

Iterazione 1

La variabile con coefficiente di costo negativo minore (-3) è x₁.

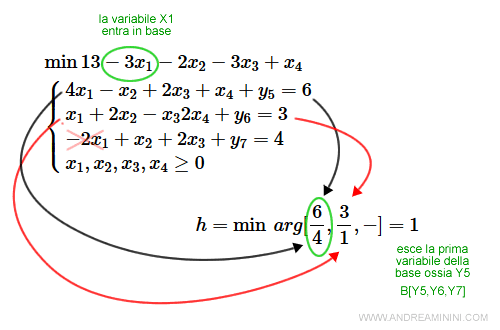
Quindi, faccio entrare in base la variabile x₁ al posto della variabile y₅ con un'operazione pivot (h,k)=(1,1).

L'elemento pivot della matrice M⁽³⁾ è a_1,1=4.

$$ M^{(4)} = Q^{(4)} \cdot M^{(3)} $$

$$ M^{(4)} = \begin{pmatrix} 1 & \frac{3}{4} & 0 & 0 \\ 0 & \frac{1}{4} & 0 & 0 \\ 0 & -\frac{1}{4} & 1 & 0 \\ 0 & \frac{1}{2} & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} -13 & -3 & -2 & -3 & 1 & 0 & 0 & 0 \\ 6 & <4> & -1 & 2 & 1 & 1 & 0 & 0 \\ 3 & 1 & 2 & -1 & -2 & 0 & 1 & 0 \\ 4 & -2 & 1 & 2 & 0 & 0 & 0 & 1 \\\end{pmatrix} $$

$$ M^{(4)} = \begin{pmatrix} -\frac{17}{2} & 0 & - \frac{11}{4} & - \frac{3}{2} & \frac{7}{4} & \frac{3}{4} & 0 & 0 \\ \frac{3}{2} & 1 & - \frac{1}{4} & \frac{1}{2} & \frac{1}{4} & \frac{1}{4} & 0 & 0 \\ \frac{3}{2} & 0 & \frac{9}{4} & -\frac{3}{2} & -\frac{9}{4} & -\frac{1}{4} & 1 & 0 \\ 7 & 0 & \frac{1}{2} & 3 & \frac{1}{2} & \frac{1}{2} & 0 & 1 \\\end{pmatrix} $$

Ora la base del problema in forma canonica è B(x₁ ,y₆ , y₇).

La soluzione non è ottima perché ci sono ancora coefficiente di costo negativi.

Iterazione 2

La variabile con coefficiente di costo negativo minore (-11/4) è x₂.

Faccio entrare in base la variabile x₂ al posto della variabile y₆ con un'operazione pivot (h,k)=(2,2).

$$ h = \min \: arg[ - , \frac{\frac{3}{2}}{\frac{9}{4}} , \frac{7}{\frac{1}{2}} ] $$

$$ h = \min \: arg[ - , \frac{3}{2} \cdot \frac{4}{9} , 7 \cdot \frac{2}{1} ] $$

$$ h = \min \: arg[ - , \frac{2}{3} , 14 ] = 2 $$

L'elemento pivot della matrice M⁽³⁾ è a_2,2=4.

$$ M^{(5)} = Q^{(5)} \cdot M^{(4)} $$

$$ M^{(5)} = \begin{pmatrix} 1 & 0 & \frac{11}{9} & 0 \\ 0 & 1 & \frac{1}{9} & 0 \\ 0 & 0 & \frac{4}{9} & 0 \\ 0 & 0 & - \frac{2}{9} & 1 \end{pmatrix} \cdot \begin{pmatrix} -\frac{17}{2} & 0 & - \frac{11}{4} & - \frac{3}{2} & \frac{7}{4} & \frac{3}{4} & 0 & 0 \\ \frac{3}{2} & 1 & - \frac{1}{4} & \frac{1}{2} & \frac{1}{4} & \frac{1}{4} & 0 & 0 \\ \frac{3}{2} & 0 &< \frac{9}{4} > & -\frac{3}{2} & -\frac{9}{4} & -\frac{1}{4} & 1 & 0 \\ 7 & 0 & \frac{1}{2} & 3 & \frac{1}{2} & \frac{1}{2} & 0 & 1 \\\end{pmatrix} $$

$$ M^{(5)} = \begin{pmatrix} -\frac{20}{3} & 0 & 0 & - \frac{10}{3} & -1 & \frac{4}{9} & \frac{11}{9} & 0 \\ \frac{5}{3} & 1 & 0 & \frac{1}{3} & 0 & \frac{2}{9} & \frac{1}{9} & 0 \\ \frac{2}{3} & 0 & 1 & -\frac{2}{3} & -1 & -\frac{1}{9} & \frac{4}{9} & 0 \\ \frac{20}{3} & 0 & 0 & \frac{10}{3} & 1 & \frac{5}{9} & -\frac{2}{9} & 1 \\\end{pmatrix} $$

Ora la base del problema in forma canonica è B(x₁ ,x₂ , y₇).

La soluzione non è ottima perché ci sono ancora coefficiente di costo negativi.

Iterazione 3

La variabile con coefficiente di costo negativo minore (-10/3) è x₃.

Faccio entrare in base la variabile x₃ al posto della variabile y₇ con un'operazione pivot (h,k)=(3,3).

$$ h = \min \: arg[ \frac{\frac{5}{3}}{\frac{1}{3}} , - , \frac{ \frac{20}{3} }{\frac{10}{3}} ] $$

$$ h = \min \: arg[ \frac{5}{3} \cdot \frac{3}{1} , - , \frac{20}{3} \cdot \frac{3}{10} ] $$

$$ h = \min \: arg[ 5 , - , 2 ] = 3 $$

L'elemento pivot della matrice M⁽³⁾ è a_3,3=10/3.

$$ M^{(6)} = Q^{(6)} \cdot M^{(5)} $$

$$ M^{(6)} = \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & - \frac{1}{10} \\ 0 & 0 & 1 & \frac{1}{5} \\ 0 & 0 & 0 & \frac{3}{10} \end{pmatrix} \cdot \begin{pmatrix} -\frac{20}{3} & 0 & 0 & - \frac{10}{3} & -1 & \frac{4}{9} & \frac{11}{9} & 0 \\ \frac{5}{3} & 1 & 0 & \frac{1}{3} & 0 & \frac{2}{9} & \frac{1}{9} & 0 \\ \frac{2}{3} & 0 & 1 & -\frac{2}{3} & -1 & -\frac{1}{9} & \frac{4}{9} & 0 \\ \frac{20}{3} & 0 & 0 & \frac{10}{3} & 1 & \frac{5}{9} & -\frac{2}{9} & 1 \\\end{pmatrix} $$

$$ M^{(6)} = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & -\frac{1}{10} & \frac{1}{6} & \frac{2}{15} & -\frac{1}{10} \\ 2 & 0 & 1 & 0 & \frac{4}{5} & 0 & \frac{2}{5} & \frac{1}{5} \\ 2 & 0 & 0 & 1 & \frac{3}{10} & \frac{1}{6} & -\frac{1}{15} & \frac{3}{10} \\\end{pmatrix} $$

Ora la base del problema in forma canonica è B(x₁ ,x₂ , x₃).

La soluzione è ottimale perché non ci sono coefficienti negativi.

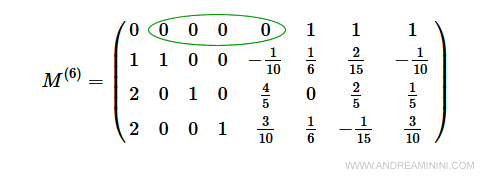
Posso quindi verificare se il problema è ammissibile oppure no.

Il problema ammette soluzioni perché la soluzione del problema artificiale ha valore nullo.

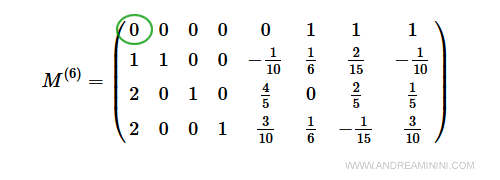
Una soluzione di base ammissibile del problema è

$$ x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 2 \\ 0 \end{pmatrix} $$

Essendo un problema ammissibile, posso passare alla fase 2 costruendo il modello in forma canonica sulla base B[1,2,3].

E poi risolverlo con l'algoritmo del simplesso.

FASE 2

Dopo aver trovato una soluzione ammissibile torno al problema originale

$$ \min 4x_1 - 2x_2 + 5_x3 \\ \begin{cases} 4x_1 - x_2 + 2x_3 + x_4 =6 \\ x_1 + 2x_2 - x_3- 2x_4 = 3 \\ -2x_1 + x_2 + 2x_3 = 4 \\ x_1, x_2, x_3,x_4 \ge 0 \end{cases} $$

e lo trasformo in forma canonica rispetto alla base B[1,2,3], quella trovata nella fase 1.

$$ \begin{cases} \min c_B^T A_B^{-1}b + c_N^T x_N \\ x_B = A_B^{-1}b - A_B^{-1} A_N x_N \\ x_B,x_N \ge 0 \end{cases} $$

Calcolo le varie componenti

$$ c_B^T=(4,-2,5) $$

$$ b = \begin{pmatrix} 6 \\ 3 \\ 4 \end{pmatrix} $$

$$ A_B =\begin{pmatrix} 4 & -1 & 2 \\ 1 & 2 & -1 \\ -2 & 1 & 2 \end{pmatrix} $$

$$ A_N =\begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} $$

$$ A^{-1}_B =\begin{pmatrix} 4 & -1 & 2 \\ 1 & 2 & -1 \\ -2 & 1 & 2 \end{pmatrix}^{-1} $$

$$ A^{-1}_B =\frac{1}{det(A)} \cdot cof \begin{pmatrix} 4 & -1 & 2 \\ 1 & 2 & -1 \\ -2 & 1 & 2 \end{pmatrix}^T $$

$$ A^{-1}_B =\frac{1}{30} \cdot cof \begin{pmatrix} 4 & -1 & 2 \\ 1 & 2 & -1 \\ -2 & 1 & 2 \end{pmatrix}^T $$

$$ A^{-1}_B =\frac{1}{30} \cdot cof \begin{pmatrix} 4 & 1 & -2 \\ -1 & 2 & 1 \\ 2 & -1 & 2 \end{pmatrix} $$

$$ A^{-1}_B =\frac{1}{30} \cdot \begin{pmatrix} 5 & 4 & -3 \\ 0 & 12 & 6 \\ 5 & -2 & 9 \end{pmatrix} $$

$$ A^{-1}_B =\begin{pmatrix} \frac{1}{6} & \frac{2}{15} & - \frac{1}{10} \\ 0 & \frac{2}{5} & \frac{1}{5} \\ \frac{1}{6} & -\frac{1}{15} & \frac{3}{10} \end{pmatrix} $$

Sostituisco i termini nella forma canonica.

$$ \begin{cases} \min(4,-2,5) \frac{1}{30} \cdot \begin{pmatrix} 5 & 4 & -3 \\ 0 & 12 & 6 \\ 5 & -2 & 9 \end{pmatrix} b = \begin{pmatrix} 6 \\ 3 \\ 4 \end{pmatrix} + c_N^T x_N \\ x_B = \frac{1}{30} \cdot \begin{pmatrix} 5 & 4 & -3 \\ 0 & 12 & 6 \\ 5 & -2 & 9 \end{pmatrix} b = \begin{pmatrix} 6 \\ 3 \\ 4 \end{pmatrix} - \begin{pmatrix} \frac{1}{6} & \frac{2}{15} & - \frac{1}{10} \\ 0 & \frac{2}{5} & \frac{1}{5} \\ \frac{1}{6} & -\frac{1}{15} & \frac{3}{10} \end{pmatrix} \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} x_4 \\ x_B,x_N \ge 0 \end{cases} $$

$$ \begin{cases} \min(4,-2,5) \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} + c_N^T x_N \\ x_B = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} - \begin{pmatrix} \frac{1}{10} \\ - \frac{4}{5} \\ \frac{3}{10} \end{pmatrix} x_4 \\ x_B,x_N \ge 0 \end{cases} $$

$$ \begin{cases} \min 10 + c_N^T x_N \\ \begin{pmatrix} x_1 \\ x_2 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} - \begin{pmatrix} \frac{1}{10} x_4 \\ - \frac{4}{5} x_4 \\ \frac{3}{10} \end{pmatrix} \\ x_1, x_2, x_3, x_4 \ge 0 \end{cases} $$

A questo punto restano da calcolare soltanto i costi ridotti

$$ c_N^T x_N = c^T - c_B^T A_B^{-1} \cdot A \cdot X $$

$$ c_N^T x_N = (4,-2,5,0) - (4,-2,5) \begin{pmatrix} \frac{1}{6} & \frac{2}{15} & - \frac{1}{10} \\ 0 & \frac{2}{5} & \frac{1}{5} \\ \frac{1}{6} & -\frac{1}{15} & \frac{3}{10} \end{pmatrix} \cdot \begin{pmatrix} 4 & -1 & 2 & 1 \\ 1 & 2 & -1 & -2 \\ -2 & 1 & 2 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} $$

$$ c_N^T x_N = (4,-2,5,0) - ( \frac{3}{2} , - \frac{3}{5}, \frac{7}{10} ) \cdot \begin{pmatrix} 4 & -1 & 2 & 1 \\ 1 & 2 & -1 & -2 \\ -2 & 1 & 2 & 0 \end{pmatrix} \cdot x_4 $$

$$ c_N^T x_N = (4,-2,5,0) - ( 4 , - 2, 5, \frac{27}{10} ) \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} $$

$$ c_N^T x_N = (0,0,0, - \frac{27}{10} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} $$

$$ c_N^T x_N = - \frac{27}{10} x_4 $$

Sostituisco i costi ridotti nel modello in forma canonica

$$ \begin{cases} \min 10 - \frac{27}{10} x_4 \\ \begin{pmatrix} x_1 \\ x_2 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} - \begin{pmatrix} \frac{1}{10} x_4 \\ - \frac{4}{5} x_4 \\ \frac{3}{10} x_4 \end{pmatrix} \\ x_1, x_2, x_3, x_4 \ge 0 \end{cases} $$

che equivale al sistema

$$ \min 10 - \frac{27}{10} x_4 \\ \begin{cases} x_1 + \frac{1}{10} x_4 = 1 \\ x_2 + \frac{4}{5} x_4 = 2 \\ x_3 - \frac{3}{10} x_4 = 2 \end{cases} \\ x_1, x_2, x_3, x_4 \ge 0 $$

Il problema non è ancora ottimale perché il coefficiente x₄ è negativo. E non è illimitato inferiormente.

E' però un buon punto iniziale per cominciare le iterazioni con il simplesso.

Nota. Nell'iterazione successiva faccio entrare in base x₄ al posto di x₂.

E così via