Gli alberi di decisione
Gli alberi di decisione ( o alberi decisionali ) sono una rappresentazione dell'apprendimento nel machine learning. Sono anche conosciuti come decision tree.
In particolar modo, gli alberi di decisione sono utilizzati nei processi di apprendimento induttivo, quelli basati sull'osservazione dell'ambiente circostante.
Come funziona un albero di decisione
Un albero di decisione è un sistema con n variabili in input e m variabili in output.
Le variabili in input ( attributi ) sono derivate dall'osservazione dell'ambiente. Le ultime variabili in output, invece, identificano la decisione / azione da intraprendere.
Nota. Negli alberi decisionali molto profondi le variabili in output intermedie, in uscita dai nodi genitori, coincidono con le variabili in input dei nodi figli. Le variabili in output intermedie condizionano il percorso verso la decisione finale.
Il processo decisionale è rappresentato con un albero logico rovesciato dove ogni nodo è una funzione condizionale.
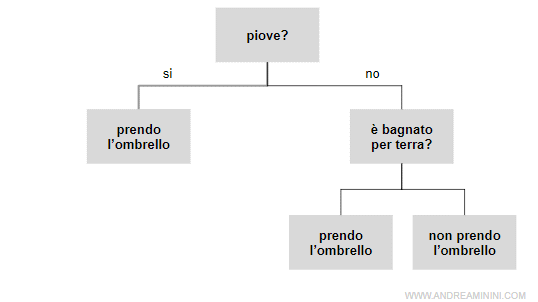
Ogni nodo verifica una condizione ( test ) su una particolare proprietà dell'ambiente ( variabile ) e ha due o più diramazioni verso il basso in funzione.
Il processo consiste in una sequenza di test. Comincia sempre dal nodo radice, il nodo genitore situato più in alto nella struttura, e procede verso il basso.
A seconda dei valori rilevati in ciascun nodo, il flusso prende una direzione oppure un'altra e procede progressivamente verso il basso.
Nota. Man mano che il processo di selezione prosegue verso il basso, lo spazio delle ipotesi si riduce perché gran parte dei rami decisionali dell'albero sono eliminati.
La decisione finale si trova nei nodi foglia terminali, quelli più in basso.
In questo modo, dopo aver analizzato le varie condizioni, l'agente giunge alla decisione finale.
Nota. Per la sua espressività e semplicità la rappresentazione ad albero decisionale è molto utilizzata anche nel marketing per costruire gli script utilizzati dai venditori e dagli operatori di telemarketing.
Tipi di alberi decisionali
In un albero decisionale le variabili possono essere:
- Variabili discrete. Le variabili hanno valori numerici interi. In questi casi si parla di classificazione.
Nota. La forma discreta più semplice è la classificazione booleana dove le variabili hanno soltanto due valori: zero ( falso ) o uno ( vero ).
- Variabili continue. Le variabili hanno valori numerici reali. Dati due numeri reali qualsiasi, c'è sempre un altro numero intermedio tra questi. In questi casi si parla di regressione.
Nota. La rappresentazione delle variabili continue è molto più complessa ma si adatta meglio alla logica sfumata ( fuzzy logic ) e alla logica in condizioni di incertezza, quando non esiste una distinzione netta tra il vero e il falso, tra un'affermazione e la sua negazione, ecc.
Pro e contro
I vantaggi
Gli alberi logici hanno l'indiscusso vantaggio della semplicità. Sono facili da capire e da eseguire.
Rispetto alle reti neurali l'albero decisionale è facilmente comprensibile dagli esseri umani.
Pertanto, l'uomo può verificare come la macchina giunge alla decisione. Eventualmente dissentire.
Esempio. Un albero decisionale applicato alla medicina fornisce delle diagnosi. Essendo una decisione importante per il paziente, è sempre opportuno che un medico verifichi il processo di classificazione che ha portato la macchina a prendere quella decisione. Per un uomo è senza dubbio più facile farlo leggendo un albero decisionale che una rete neurale.
Potrebbero anche esistere criteri decisionali più efficienti, più adatti alla logica delle macchine ma meno comprensibili dall'uomo.
E' un aspetto da non sottovalutare.
Inoltre, gli alberi decisionali booleani sono facilmente sviluppabili sotto forma di codice di programmazione, perché possono essere rappresentati con qualsiasi linguaggio proposizionale.
Nota. Tutte le funzioni booleane possono essere rappresentate come albero di decisionale. E viceversa.
Questa caratteristica è detta espressività degli alberi decisionali.
Un esempio pratico
Il seguente albero è composto da due attributi o test ( A, B ) e un valore booleano in uscita ( Yes / No ) alla funzione PrendoOmbrello(s).
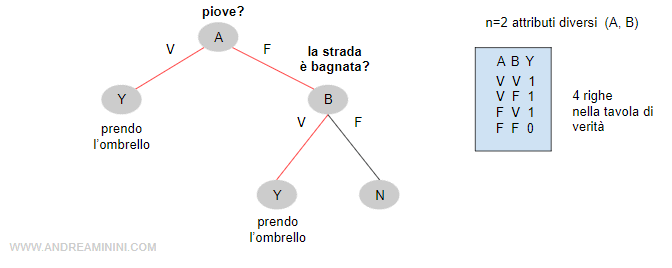
Nel linguaggio proposizionale la funzione di verità PrendoOmbrello(s) può essere scritta nel seguente modo:

La proposizione individua i due cammini possibili nell'albero decisionale che consentono di raggiungere il nodo terminale Y a partire dalla radice, ossia i nodi dove la funzione PrendoOmbrello è vera ossia ha valore uguale a 1.
Spiegazione. Per ogni stato (s) la funzione PrendoOmbrello è vera se la proposizione 1 o la proposizione 2 è vera. Uno stato (s) è una combinazione di valori che possono assumere i due attributi A e B. Ogni stato è un vettore che coincide con una determinata riga della tavola di verità e con un determinato cammino dalla radice a una foglia terminale con esito positivo (Y).
Gli svantaggi
La rappresentazione ad albero decisionale è poco adatta per i problemi complessi, perché lo spazio delle ipotesi diventa troppo grande.
La complessità spaziale dell'algoritmo potrebbe diventare proibitiva.
Esempio. Nel caso più semplice di un albero booleano, per n attributi in input ( es. le variabili in input A, B, C) occorrono 2n combinazioni ( cammini nelle ramificazioni ) ossia 2n righe in una tavola di verità per determinare la decisione finale ( Y / N ). Tuttavia, se un nodo avesse più attributi ( numero classi = numero rami in uscita ) o fosse una variabile non booleana ( es. temperatura ), le combinazioni sarebbero decisamente molte di più.
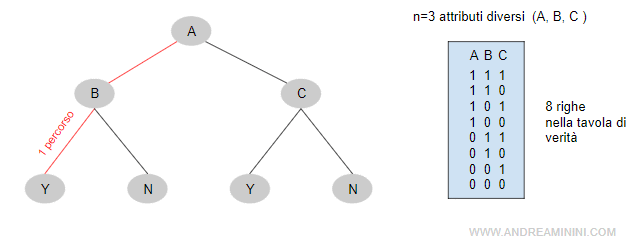
Un albero decisionale può descrivere soltanto una relazione tra una funzione di verità e le combinazioni logiche di attributi. Non riesce a rappresentare più funzioni.
Per farlo occorre creare un altro albero decisionale e associarlo al precedente.
Ogni funzione di verità è un albero decisionale a se stante.
Inoltre, l'albero decisionale non riesce a rappresentare tutti i tipi di funzioni ma soltanto alcuni.
Esempio. L'albero di decisione non riesce a rappresentare una funzione che restituisce 1 quando tutti gli attributi sono veri ( funzione di parità ) o quando la maggioranza degli attributi sono veri ( funzioni di maggioranza ).
