Algoritmo Adaline online
Questo algoritmo è una versione di Adaline con discesa del gradiente online. E' un algoritmo di classificazione lineare per l'apprendimento con supervisione ( machine learning ). E' anche detto a discesa stocastica o iterativa ( Stochastic Gradient Descent – SGD ).
Qual è la differenza tra Adaline classico e online? L'algoritmo classico di Adaline aggiorna tutti i pesi al termine di ogni epoch in base alla somma degli errori cumulati su tutti i campioni. La versione online, invece, li aggiorna dopo ogni esempio (campione) in modo incrementale, senza dover aggiornare tutto il dataset ogni volta. E' quindi più efficiente.

Tasso di apprendimento adattivo
Il tasso di apprendimento nella versione online di Adaline è di tipo adattivo, ossia non è fisso ma viene modificato nel corso dell'elaborazione.
In particolar modo, il tasso di apprendimento η si riduce nel corso del tempo.
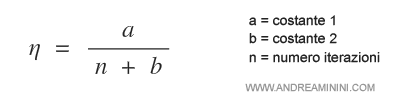
Spiegazione. Le costanti a e b sono gli iperparametri del processo di learning. A seconda della configurazione del rapporto a/b la variazione del tasso di apprendimento è più rapida o più lenta. La variabile n è, invece, il numero di iterazioni dell'algoritmo nel corso del processo di apprendimento.
Questo consente di migliorare le performance del processo di learning.
Come programmare Adaline online con python
Apro l'editor idle di python e importo le librerie che mi servono.
import pandas as pd
import numpy as np
import matplotlib.pyplot as mpl
from numpy.random import seed
Poi scelgo il dataset da analizzare.
Opto per il classico dataset Iris.
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
df.tail()
Semplifico il dataset assegnando -1 alle etichette "Iris-setosa" e 1 a tutte le altre ( non Iris-setosa ).
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
x = df.iloc[0:100, [0, 2]].values
Standardizzo la variabile degli esempi per aumentare l'efficienza computazionale
x_std = np.copy(x)
x[:,0] = (x[:,0] - x[:,0].mean()) / x[:,0].std()
x[:,1] = (x[:,1] - x[:,1].mean()) / x[:,1].std()
Poi inizializzo a zero il vettore dei pesi
w_ = np.zeros(1 + x.shape[1])
Inizializzo a zero anche il vettore dei costi storici dove registrerò il costo dopo ogni esempio
cost_ = []
Definisco gli iperparametri dell'algoritmo ossia eta (tasso di apprendimento) ed epoch (numero dei cicli).
eta=0.01
epoch=50
Scelgo un seme per la randomizzazione.
Mi servirà per scegliere casualmente un esempio da analizzare.
seed(1)
A questo punto manca soltanto la routine dell'algoritmo di apprendimento.
E' una routine composta da un ciclo esterno (riga 1) e un ciclo interno (riga 6).
- for i in range(0,epoch):
- r = np.random.permutation(len(y))
- xx=x[r]
- yy=y[r]
- cost = []
- for xi, target in zip(xx, yy):
- output = np.dot(xi, w_[1:]) + w_[0]
- error = (target - output)
- w_[1:] += eta * xi.dot(error)
- w_[0] += eta * error
- costx=0.5 * error**2
- cost.append(costx)
- avg_cost = sum(cost)/len(yy)
- print(i, avg_cost)
- costostorico.append(avg_cost)
Come funziona?
Il ciclo esterno compie 50 iterazioni ( epoch ).
Nella riga 2 crea un vettore con y permutazioni casuali degli esempi del dataset.
Il contenuto della variabile r è il seguente:
array([80, 84, 33, 81, 93, 17, 36, 82, 69, 65, 92, 39, 56, 52, 51, 32, 31,
44, 78, 10, 2, 73, 97, 62, 19, 35, 94, 27, 46, 38, 67, 99, 54, 95,
88, 40, 48, 59, 23, 34, 86, 53, 77, 15, 83, 41, 45, 91, 26, 98, 43,
55, 24, 4, 58, 49, 21, 87, 3, 74, 30, 66, 70, 42, 47, 89, 8, 60,
0, 90, 57, 22, 61, 63, 7, 96, 13, 68, 85, 14, 29, 28, 11, 18, 20,
50, 25, 6, 71, 76, 1, 16, 64, 79, 5, 75, 9, 72, 12, 37])
Poi nelle righe 3 e 4 assegna alle variabili xx e yy l'esempio r del dataset.
Dove xx è la matrice degli esempi e yy è il vettore delle etichette dell'esempio ( soluzione corretta ).
Nella riga 5 inizializzo a zero il vettore dei costi dell'esempio ( cost[] ).
Per ogni epoch ( 50 cicli ) l'algoritmo esegue un ciclo interno ( riga 6 ) che legge ogni singolo esempio e soluzione di zip(xx,yy) e li assegna alle variabili interne xi e target
La funzione zip() unisce la matrice degli esempi xx con il vettore delle etichette yy.
Ad esempio, alla prima iterazione xi ha questo valore
[0.04542025 0.65079974]
mentre target ha questo valore
1
La riga 7 calcola il prodotto tra il vettore dell'esempio (xi) e il vettore dei pesi w.
Poi assegna il risultato alla variabile output
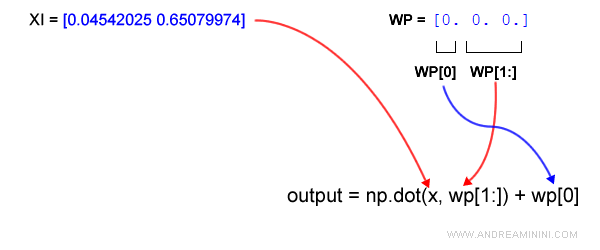
Il vettore dei pesi è inizialmente a zero.
Quindi, alla variabile output viene assegnato il valore 0.
Nella riga 8 l'algoritmo confronta la variabile output con l'etichetta (target) dell'esempio.
Poi assegna il risultato alla variabile error.
error = (target - output)
In questo caso l'etichetta dell'esempio è 1 mentre la variabile output è 0.
Quindi, la variabile error è uguale a 1-0 ossia 1.
Nota. Se il risultato (output) fosse corretto, ossia uguale a target, la variabile error sarebbe uguale a 0. I pesi non si aggiornerebbero e non verrebbe generato alcun errore dall'esempio.
La riga 9 calcola i nuovi pesi wp[] a partire dal secondo elemento [1:] in poi.
Il primo elemento wp[0] è usato per registrare l'errore totale.
w_[1:] += eta * xi.dot(error)
La variabile eta (0.01) viene moltiplicata per il prodotto del vettore xi con l'errore (error=1) tramite la funzione dot().
Il risultato viene aggiunto (+=) al vettore w_[1:]
w_[1:] += 0.01 * [0.04542025, 0.65079974]*1
ossia
w_[1:] += [0.0004542, 0.006508 ]
La riga 10 moltiplica l'errore (error) per il primo elemento del vettore dei pesi w_[0] e incrementa quest'ultimo.
w_[0] += eta * error
Quindi
w_[0] += 0.01 * 1
La riga 11 è la funzione di costo dell'esempio.
costx=0.5 * error**2
Il costo dell'esempio è
costx=0.5 * 1**2 = 0.5
Nella riga 12 il costo dell'esempio (costx) viene aggiunto al vettore dei costi (cost)
cost.append(costx)
Il ciclo interno ricomincia con l'esempio seguente.
Alla fine del ciclo interno, dopo y iterazioni (100 esempi), il vettore cost contiene i costi calcolati in ogni elemento
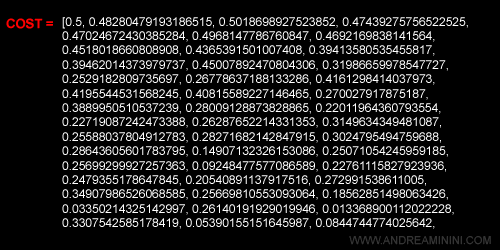
Come si può vedere, il costo tende a scendere man mano che si elaborano i 100 esempio.
Questo è dovuto al fatto che i pesi sono aggiornati dopo ogni singolo esempio.
Nota. Questa è la differenza sostanziale tra l'algoritmo Adaline online e l'algoritmo classico di Adaline.
La riga 13 calcola la media dei costi e la assegna alla variabile avg_cost
avg_cost = sum(cost)/len(yy)
La riga 14 stampa il valore della variabile avg_cost tramite l'istruzione print.
Al primo ciclo esterno (epoch=1) la variabile avg_cost vale
0.20186244689789765
Infine, la riga 15 aggiunge il costo medio della prima epoch al vettore dei costi storici.
Il ciclo esterno passa all'iterazione successiva (epoch=2).
In questo caso, però, il vettore dei pesi w_ non è più nullo perché viene ereditato dalla epoch=1.
array([0.00144482, 0.27128993, 0.50633398])
Il ciclo itera allo stesso modo per cinquanta volte fino a epoch=50.
In questa tabella sono sintetizzati i pesi e il costo medio in ogni epoch.
| epoch | avg_cost |
|---|---|
| 0 | 0.20186244689789765 |
| 1 | 0.07234684958431871 |
| 2 | 0.05563818786373788 |
| 3 | 0.045629378796776206 |
| 4 | 0.039047824048889866 |
| 5 | 0.034581262742869476 |
| 6 | 0.031546371851303386 |
| 7 | 0.029465877618589806 |
| 8 | 0.028053254570522622 |
| 9 | 0.02702199335257547 |
| 10 | 0.026231122300635037 |
| 11 | 0.025818702327018345 |
| 12 | 0.025483332122000994 |
| 13 | 0.025230404849847447 |
| 14 | 0.025104142841814753 |
| 15 | 0.02507708523362468 |
| 16 | 0.025020716959835355 |
| 17 | 0.02494815271593558 |
| 18 | 0.02482979097334819 |
| 19 | 0.024927278732124924 |
| 20 | 0.024612835873063624 |
| 21 | 0.0248169675401525 |
| 22 | 0.024907289020746265 |
| 23 | 0.024920971578863114 |
| 24 | 0.024934732048547882 |
| 25 | 0.024914986261020046 |
| 26 | 0.024940685049010217 |
| 27 | 0.024920120890807942 |
| 28 | 0.024928678920114255 |
| 29 | 0.024785775656241654 |
| 30 | 0.02483189121119823 |
| 31 | 0.0247965090048165 |
| 32 | 0.024893128300383795 |
| 33 | 0.024877306143306042 |
| 34 | 0.024887864818428543 |
| 35 | 0.024744795801649497 |
| 36 | 0.024917535062296502 |
| 37 | 0.02487841286896553 |
| 38 | 0.024908242039408383 |
| 39 | 0.024844810838095244 |
| 40 | 0.024937639440709872 |
| 41 | 0.0248816539615484 |
| 42 | 0.024562466389100188 |
| 43 | 0.02495174159829769 |
| 44 | 0.024927410437265415 |
| 45 | 0.02479207399102695 |
| 46 | 0.024919729011427753 |
| 47 | 0.024878167152841343 |
| 48 | 0.024817909408501416 |
| 49 | 0.02491726394970519 |
Il costo medio è sceso rapidamente nelle prime 7-8 epoch per poi stabilizzarsi intorno 0.024 fino alla 50a epoch.
Aggiungo altre due righe alla fine dello script per rappresentare l'andamento del costo medio su un diagramma cartesiano
plt.plot(costostorico, color = 'red')
plt.show()
Il grafico mostra l'andamento del costo medio dalla prima all'ultima epoch (50)
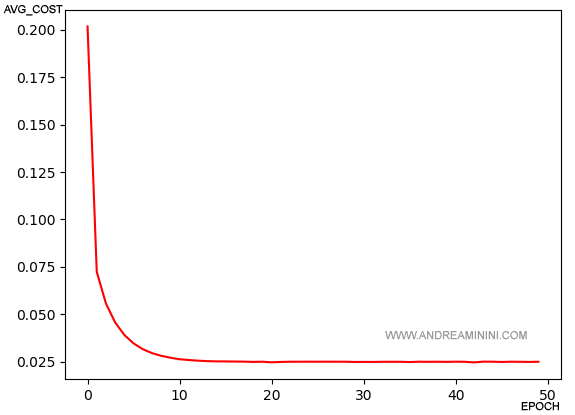
In poche epoch l'algoritmo Adaline online raggiunge un buon risultato, molto prima rispetto all'algoritmo Adaline classico.
Perché?
Il costo scende rapidamente perché l'aggiornamento dei pesi è più frequente rispetto ad Adaline classico, è calcolato dopo ogni singolo esempio e non al termine di ogni epoch.
Così facendo, l'algoritmo viene addestrato più velocemente alla classificazione degli esempi
Pro e contro di Adaline online
I vantaggi
La versione online di Adaline è sicuramente più efficiente rispetto ad Adaline classico, converge più velocemente all'obiettivo perché non deve aggiornare l'intero dataset dopo ogni passo in avanti.
E' particolarmente utile nei casi in cui il dataset non è predefinito ma si forma nel corso del tempo.
Esempio. Se la macchina deve essere addestrata osservando gli eventi man mano che si verificano. In questo caso, non c'è uno stock di esempi già pronto da analizzare ( training set ) ma un flusso continuo di esempi ( addestramento online ).
Inoltre, se l'algoritmo elabora un flusso di esempi non ha bisogno di memorizzare gli esempi e si riduce la complessità spaziale dell'algoritmo, ossia lo spazio di memoria usato necessario per far girare il programma.
Gli svantaggi
L'algoritmo Adaline online fornisce risultati più approssimativi rispetto ad Adaline classico.
E' inoltre più soggetto al problema del rumore nei dati.
L'approccio incrementale espone l'algoritmo anche al problema dei minimi locali e al ripetersi degli stessi cicli.
Soluzione. Per evitare questi ultimi due problemi posso randomizzare il dataset dopo ogni epoch, modificando l'ordine degli esempi nell'insieme di addestramento in modo casuale.
