Adaline
L'algoritmo Adaline ( ADAptive LInear NEuron ) è un modello di classificazione convergente basato sull'utilizzo di neuroni artificiali adattivi lineari.
Chi l'ha inventato? E' stato sviluppato da Bernard Widrow e Tedd Hoff nel 1960. E' un'evoluzione del modello del Perceptron. Il modello di riferimento è sempre il neurone MCP di McCullock, Pitts, Rosenblatt.
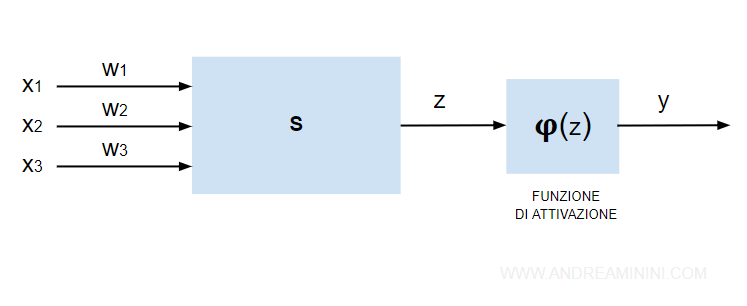
Si tratta di una tecnica di apprendimento automatico (machine learning) con supervisione.
Le caratteristiche di Adaline
Le principali caratteristiche dell'algoritmo Adaline sono le seguenti:
- L'algoritmo Adaline minimizza una funzione J durante l'apprendimento.
- La funzione di attivazione φ dei neuroni è continua e lineare.
- L'aggiornamento dei pesi (w) viene calcolato in batch ( a lotti ) su tutti gli esempi dell'insieme di apprendimento.
La differenza tra Perceptron e Adaline. Nel Perceptron, i pesi erano aggiornati in modo incrementale dopo ogni campione. Inoltre, la funzione era binaria con due soli stati ( 0 oppure 1 ).
Come funziona l'algoritmo Adaline
L'obiettivo dell'algoritmo è minimizzare una funzione obiettivo J(w).
Dove z è il vettore dei pesi wT x(i) mentre Y(i) è l'output della macchina.
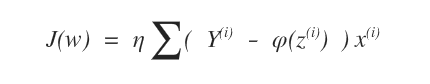
La funzione J(w) somma la differenza assoluta ( gradiente ) dovuta all'errore (Y-φ) tra la risposta della macchina e quella negli esempi di training.
Pertanto, quanto più è basso il valore della funzione J(w), tanto più è affidabile il modello previsionale.
Nota. I pesi dei neuroni (w) sono aggiornati in base all'entità reale dell'errore tra il risultato atteso dagli esempi e l'output del programma.
Il parametro η è il tasso di apprendimento. E' un iperparametro particolarmente importante perché influisce sulla velocità di apprendimento e sull'efficacia dell'algoritmo.
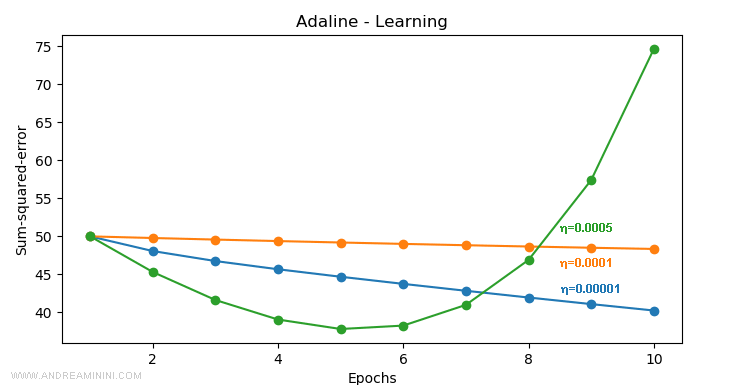
Nota. Se il parametro η è troppo basso (es. η=0,00001 ) la velocità di apprendimento si riduce eccessivamente. Sono necessarie molte epoch (cicli) per ridurre gli errori. Se invece è troppo alto (es. η=0,0005 ), il numero degli errori può anche aumentare anziché ridursi.
Come programmare Adaline in python
Per capire meglio il funzionamento dell'algoritmo provo a svilupparlo in linguaggio python.
Questo mi permette anche di osservare più da vicino alcune sue criticità.
Apro l'editor di python e importo le librerie pandas, numpy
import pandas as pd
import numpy as np
Poi definisco il training set usando il classico esempio Iris.
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
df.tail()
Semplifico il training set per distinguere gli esempi con etichetta "Iris-Setosa" da tutte le altre etichette.
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
x = df.iloc[0:100, [0, 2]].values
Creo il vettore a zero dei pesi con tre elementi.
wp = np.zeros(1 + x.shape[1])
Pertanto, inizialmente il contenuto del vettore wp è il seguente:
[0., 0., 0.]
Creo il vettore dei costi a zero
cost_ = []
Poi definisco gli iperparametri del programma ( eta, epoch ).
Dove eta è il tasso di apprendimento η della formula precedente, mentre epoch è il numero delle iterazioni (50) del programma.
eta=0.0005
epoch=50
La routine di apprendimento vera e propria è la seguente:
- for i in range(0,epoch):
- output = np.dot(x, wp[1:]) + wp[0]
- errors = (y - output)
- wp[1:] += eta * x.T.dot(errors)
- wp[0] += eta * errors.sum()
- cost = (errors**2).sum() / 2.0
- cost_.append(cost)
Si tratta di un ciclo for con 50 iterazioni ( epoch ).
Come funziona?
La riga 2 calcola l'output del programma.
output = np.dot(x, wp[1:]) + wp[0]
E' un prodotto tra la matrice x degli esempi e il vettore dei pesi wp tramite la funzione dot() di numpy.
Inizialmente i pesi sono tutti a zero.
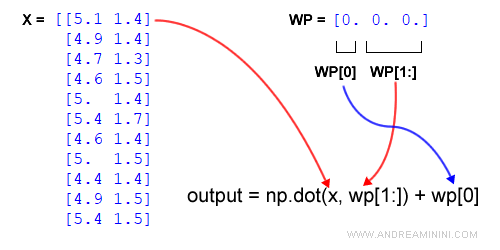
Il risultato viene assegnato alla variabile output.
Al primo ciclo la variabile output è una matrice di zeri.
output= [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0.]
La riga 3 confronta il vettore y delle etichette del training set con il vettore dell'output del programma.
errors = (y - output)
La differenza tra i due vettori y-output viene registrata nel vettore errors.
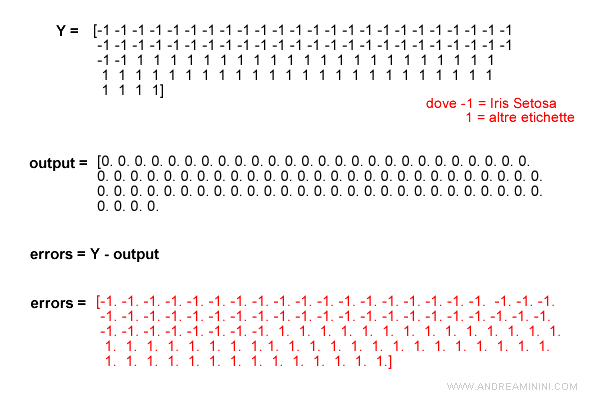
La riga 4 calcola i nuovi pesi da aggiungere al vettore wp[] a partire dal secondo elemento [1:] in poi.
Il primo elemento wp[0] è usato per registrare l'errore totale.
wp[1:] += eta * x.T.dot(errors)
Questa riga di codice calcola la matrice trasposta ( x.T ) della matrice X degli esempi.

Poi calcola il prodotto riga per colonna della matrice trasposta (x.T) per il vettore degli errori (errors) tramite la funzione dot().
Il risultato è un vettore composto da due elementi.

Il risultato del prodotto viene moltiplicato per la variabile eta ( tasso di apprendimento ).
In questo caso eta è uguale a 0.0005
eta*[ 46.5 139.8]
0.0005*[ 46.5 139.8]
[ 0.0005*46.5 0.0005*139.8]
[0.02325 0.0699 ]
Pertanto
wp[1:] +=[0.02325 0.0699 ]
La riga 5 somma gli errori commessi durante l'epoch e li moltiplica per il tasso di apprendimento eta (0.0005).
Il risultato viene aggiunto al primo elemento del vettore wp.
wp[0] += eta * errors.sum()
A questo punto il vettore dei pesi wp è il seguente:
array([0. , 0.02325, 0.0699 ])
La riga 6 calcola il costo dell'epoch.
Somma (sum) gli errori elevati al quadrato (errors*2) e divide per due la somma.
cost = (errors**2).sum() / 2.0
In questo caso, nella prima epoch il costo complessivo è pari a 50
La riga 7 aggiunge il costo appena calcolato alla lista cost_ che mi permette di vedere l'evoluzione della funzione costo in tutte le epoch (cicli) del programma
cost_.append(cost)
Il ciclo viene ripetuto per 50 volte.
Ecco l'evoluzione delle variabilie cost (costo) ed errors (somma degli errori) durante i vari cicli (epoch).
| Epoch | Cost | Errors |
|---|---|---|
| 0 | 50.0 | 0 |
| 1 | 45.142 | -32 |
| 2 | 40.815 | 2 |
| 3 | 36.964 | -31 |
| 4 | 33.538 | 5 |
| 5 | 30.492 | -31 |
| 6 | 27.786 | 7 |
| 7 | 25.385 | -31 |
| 8 | 23.256 | 9 |
| 9 | 21.372 | -30 |
| 10 | 19.706 | 11 |
| 11 | 18.236 | -30 |
| 12 | 16.943 | 13 |
| 13 | 15.808 | -31 |
| 14 | 14.814 | 15 |
| 15 | 13.949 | -31 |
| 16 | 13.2 | 17 |
| 17 | 12.554 | -31 |
| 18 | 12.003 | 19 |
| 19 | 11.537 | -32 |
| 20 | 11.149 | 21 |
| 21 | 10.832 | -33 |
| 22 | 10.579 | 23 |
| 23 | 10.385 | -34 |
| 24 | 10.246 | 25 |
| 25 | 10.157 | -35 |
| 26 | 10.116 | 27 |
| 27 | 10.117 | -36 |
| 28 | 10.16 | 29 |
| 29 | 10.241 | -37 |
| 30 | 10.359 | 31 |
| 31 | 10.513 | -38 |
| 32 | 10.7 | 33 |
| 33 | 10.919 | -40 |
| 34 | 11.17 | 35 |
| 35 | 11.453 | -41 |
| 36 | 11.767 | 37 |
| 37 | 12.111 | -43 |
| 38 | 12.485 | 40 |
| 39 | 12.891 | -45 |
| 40 | 13.327 | 42 |
| 41 | 13.795 | -47 |
| 42 | 14.295 | 44 |
| 43 | 14.827 | -49 |
| 44 | 15.394 | 47 |
| 45 | 15.995 | -52 |
| 46 | 16.631 | 50 |
| 47 | 17.305 | -54 |
| 48 | 18.017 | 52 |
| 49 | 18.769 | -57 |
L'algoritmo Adaline ha effettivamente ridotto il costo della funzione.
Ci sono però alcune osservazioni importanti da fare
- La funzione di costo è scesa troppo lentamente. Il processo di ottimizzazione è ancora lungo. Questo dire che la configurazione degli iperparametri è migliorabile.
- Il costo ha cominciato a crescere a partire dalla epoch=26. La funzione previsionale stimata alla ventiseiesima epoch (c=10.1) era più efficiente rispetto a quella finale (c=18.7)
- Dopo ogni epoch il numero degli errori è rimbalzato nel gradiente da una parte all'altra come un pendolo. Ad esempio, da 40 a -45, poi da -45 a 42. Non converge verso il costo minimo assoluto. E' un handicap dell'algoritmo.
Nota. Per evitare questo problema dovrei settare un tasso di apprendimento (eta) con un valore più basso. Ad esempio, η=0,0001 al posto di η=0,0005 Questo però allungherebbe notevolmente il numero dei cicli (epoch) necessari per ridurre la funzione di costo.
In conclusione, l'algoritmo Adaline funziona ma presenta un elevato rischio di inefficienza.
Inoltre, se gli iperparametri non sono settati in modo ottimale, l'algoritmo diventa anche inefficace.
Esempio. Fissando 100 epoch l'algoritmo estrapola una funzione di costo pari c=192. Praticamente il quadruplo rispetto al costo iniziale (C=50).
Questi problemi possono comunque essere eliminati tramite la standardizzazione delle variabili.
La standardizzazione risolve qualche problema
Per standardizzare le variabili aggiungo queste righe di codice all'inizio del programma:
Vanno inserite subito dopo aver definito la variabile x.
x[:,0] = (x[:,0] - x[:,0].mean()) / x[:,0].std()
x[:,1] = (x[:,1] - x[:,1].mean()) / x[:,1].std()
Dove l'attributo mean è la media aritmetica e std è la deviazione standard.
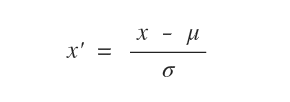
Questa modifica rende gli errori infinitesimali e la funzione di costo si riduce più rapidamente.
In soli 8 cicli ( epoch ) anziché 50 raggiunge lo stesso risultato (C≅18) della precedente versione dell'algoritmo.
| Epoch | Cost | Errors |
|---|---|---|
| 0 | 50.0 | 0 |
| 1 | 42.971 | 0 |
| 2 | 37.136 | 0 |
| 3 | 32.289 | 0 |
| 4 | 28.259 | 0 |
| 5 | 24.904 | 0 |
| 6 | 22.11 | 0 |
| 7 | 19.778 | 0 |
| 8 | 17.83 | 0 |
| 9 | 16.2 | 0 |
| 10 | 14.832 | 0 |
| 11 | 13.682 | 0 |
| 12 | 12.712 | 0 |
| 13 | 11.892 | 0 |
| 14 | 11.196 | 0 |
| 15 | 10.603 | 0 |
| 16 | 10.095 | 0 |
| 17 | 9.658 | 0 |
| 18 | 9.28 | 0 |
| 19 | 8.952 | 0 |
| 20 | 8.664 | 0 |
| 21 | 8.41 | 0 |
| 22 | 8.185 | 0 |
| 23 | 7.983 | 0 |
| 24 | 7.802 | 0 |
| 25 | 7.638 | 0 |
| 26 | 7.487 | 0 |
| 27 | 7.349 | 0 |
| 28 | 7.221 | 0 |
| 29 | 7.102 | 0 |
| 30 | 6.99 | 0 |
| 31 | 6.884 | 0 |
| 32 | 6.784 | 0 |
| 33 | 6.689 | 0 |
| 34 | 6.598 | 0 |
| 35 | 6.51 | 0 |
| 36 | 6.426 | 0 |
| 37 | 6.345 | 0 |
| 38 | 6.267 | 0 |
| 39 | 6.191 | 0 |
| 40 | 6.117 | 0 |
| 41 | 6.045 | 0 |
| 42 | 5.975 | 0 |
| 43 | 5.907 | 0 |
| 44 | 5.84 | 0 |
| 45 | 5.775 | 0 |
| 46 | 5.712 | 0 |
| 47 | 5.65 | 0 |
| 48 | 5.589 | 0 |
| 49 | 5.529 | 0 |
Essendo variabili standardizzate, gli errori sono valori numerici molto piccoli. Per questa ragione nella colonna c'è lo zero.
Aumentando il numero delle epoch non si corre più alcun rischio.
Attenzione. In ogni caso, la modifica non elimina il problema del tasso di apprendimento. Se l'iperparametro eta è troppo grande, la funzione di costo diverge all'infinito anziché convergere verso il minimo globale.
Pro e contro dell'algoritmo
L'algoritmo Adaline raggiunge il risultato ma in modo meno efficiente rispetto ad altri.
E' fortemente dipendente dagli iperparametri ( epoch e tasso di apprendimento ). Se sono sbagliati l'algoritmo diverge anziché convergere sulla soluzione.
L'algoritmo Adaline utilizza un algoritmo a discesa del gradiente batch, aggiorna tutti i dati di addestramento per ogni passo in avanti. Se il dataset è molto grande, la complessità computazionale dell'algoritmo può diventare eccessiva.
Soluzione. Quest'ultimo problema si risolve in due modi usando una versione di Adaline con discesa del gradiente online che aggiorna i pesi in modo incrementale, più frequentemente, per ogni esempio. In alternativa, si può suddividere il dataset in sottoinsiemi ed elaborare ognuno come mini-batch tramite Adaline con discesa del gradiente batch.
