Perceptron con scikit learn in python

Questo script esegue il classificatore Perceptron ( machine learning ) tramite la libreria scikit-learn del linguaggio python.

Su quale dataset? Nello script importo il dataset iris direttamente dalla collezione integrata nella libreria scikit-learn (riga 7). Il 30% degli esempi lo utilizzo come test set (riga 10) mentre il restante 70% come training set.

I dati sono standardizzati prima dell'elaborazione.

1. import numpy as np
2. from sklearn import datasets
3. from sklearn.linear_model import Perceptron
4. from sklearn.metrics import accuracy_score
5. from sklearn.model_selection import train_test_split
6. # preparazione dataset
7. iris = datasets.load_iris()
8. X = iris.data[:, [2, 3]]
9. y = iris.target
10. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
11. # standardizzazione
12. from sklearn.preprocessing import StandardScaler
13. sc = StandardScaler()
14. sc.fit(X_train)
15. X_train_std = sc.transform(X_train)
16. X_test_std = sc.transform(X_test)
17. # addestramento
18. ppn = Perceptron(max_iter=40, tol=0.001, eta0=0.01, random_state=0)
19. ppn.fit(X_train_std, y_train)
20. # test e calcolo accuratezza
21. y_pred = ppn.predict(X_test_std)
22. print(accuracy_score(y_test, y_pred))

Gli iperparametri

Nella riga 7 eseguo il metodo fit() fissando il numero massimo di iterazioni (max_iter) a 40 e una tolleranza di uscita (tol) a 0.001.

Fisso il tasso di apprendimento (eta0) del modello di apprendimento a 0.01

L'accuratezza

Lo script ha un'accuratezza del 97%

0.9777777777777777

Vuol dire che dopo l'addestramento il modello prevede e classifica correttamente il 97% degli esempi dell'insieme di test.

Rappresentazione grafica del classificatore

Aggiungo qualche riga in fondo allo script python per rappresentare graficamente la classificazione del Perceptron con la funzione plot_decision_region().

1. from mlxtend.plotting import plot_decision_regions
2. # Plotting decision regions
3. plot_decision_regions(X_test, y_test, clf=ppn, legend=2)
4. # Adding axes annotations
5. import matplotlib.pyplot as plt
6. plt.show()

La funzione mostra la ripartizione degli esempi di test.

Sugli assi x e y sono misurati i valori dei due attributi degli esempi.

I simboli (quadrato, triangolo, cerchio) indicano le diverse tipologie di fiori Iris ( versicolor, setosa, virginica ).

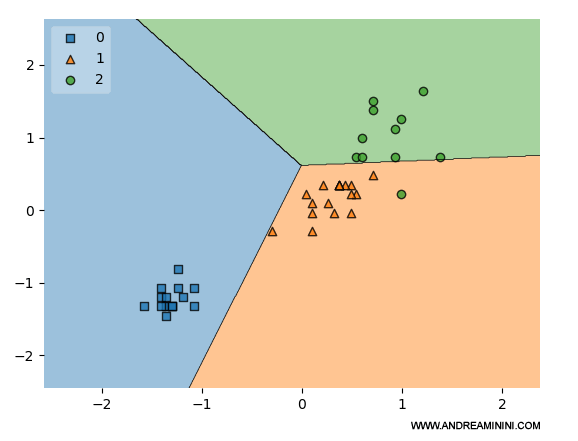
Il modello ha diviso correttamente la regione degli esempi dell'insieme di test in tre parti distinte. C'è un solo errore.

Nota. Uno dei limiti del percpetron è di non riuscire a riconoscere regioni non delimitate in modo lineare. In questo caso, il dataset Iris è molto semplice ed è stato possibile farlo.

Verifica

Per verificare il risultato aggiungo in coda allo script un ciclo per leggere i singoli esempi di test (standardizzati) e calcolare l'etichetta tramite il classificatore.

1. for i in range(0,len(X_test_std)):
2. z = np.array([X_test_std[i]])
3. y = ppn.predict(z)
4. print(X_test_std[i], y_test[i], y)

Il risultato è il seguente:

num	X_test_std	y_test	predict()
1	[0.70793846 1.51006688]	2	2
2	[ 0.09545238 -0.29318114]	1	1
3	[-1.35224199 -1.32360858]	0	0
4	[1.37610509 0.7372463 ]	2	2
5	[-1.29656144 -1.32360858]	0	0
6	[1.20906343 1.63887031]	2	2
7	[-1.40792255 -1.19480515]	0	0
8	[0.48521625 0.35083601]	1	1
9	[0.5408968 0.22203258]	1	1
10	[0.09545238 0.09322915]	1	1
11	[0.98634122 0.22203258]	2	1
12	[0.37385514 0.35083601]	1	1
13	[ 0.48521625 -0.03557428]	1	1
14	[0.42953569 0.35083601]	1	1
15	[0.48521625 0.22203258]	1	1
16	[-1.35224199 -1.45241201]	0	0
17	[0.37385514 0.35083601]	1	1
18	[ 0.31817459 -0.03557428]	1	1
19	[-1.35224199 -1.19480515]	0	0
20	[-1.40792255 -1.06600172]	0	0
21	[0.59657735 0.99485316]	2	2
22	[0.37385514 0.35083601]	1	1
23	[-1.07383923 -1.32360858]	0	0
24	[-1.35224199 -1.32360858]	0	0
25	[0.5408968 0.7372463]	2	2
26	[-1.57496421 -1.32360858]	0	0
27	[-1.07383923 -1.06600172]	0	0
28	[0.26249403 0.09322915]	1	1
29	[-0.29431149 -0.29318114]	1	1
30	[-1.24088089 -1.06600172]	0	0
31	[0.93066067 0.7372463 ]	2	2
32	[0.37385514 0.35083601]	1	1
33	[-1.29656144 -1.32360858]	0	0
34	[0.59657735 0.7372463 ]	2	2
35	[0.98634122 1.25246002]	2	2
36	[0.03977182 0.22203258]	1	1
37	[-1.18520034 -1.19480515]	0	0
38	[0.70793846 0.47963944]	1	1
39	[0.20681348 0.35083601]	1	1
40	[ 0.09545238 -0.03557428]	1	1
41	[0.93066067 1.12365659]	2	2
42	[-1.40792255 -1.32360858]	0	0
43	[0.70793846 1.38126345]	2	2
44	[-1.24088089 -0.80839486]	0	0
45	[-1.29656144 -1.32360858]	0	0

Su 45 esempi presenti nel test set, il classificatore ha sbagliato un solo esempio, l'esempio numero 11.

Il modello ha un tasso di errore di 1/45 = 0.0222 ossia del 2,22% periodico

Questo equivale a dire che il modello ha un'accuratezza di circa il 97,78%.

Il dato conferma il risultato ottenuto in precedenza con il metodo accuracy_score().

E così via.