Come fare l'analisi dei residui del regressore con scikit learn
Dopo aver creato un modello di regressione con il machine learning supervisionato, valuto la qualità previsionale del modello tramite le metriche che analizzano i residui.
Cos'è un residuo? E' la differenza tra il valore previsto dal modello (y) e il valore corretto dell'esempio nel dataset di test (variabile target).
Le metriche di scikit learn
Scikit learn mette a disposizione diverse metriche utili:
- mean_absolute_error(y_test,p)
- mean_squared_error(y_test,p)
- r2_score(y_test,p)
Per un approfondimento sulle metriche della regressione.
Un esempio pratico
Questo codice python crea un modello di regressione elaborando in input il dataset di training "Boston" sui prezzi delle case.
Come algoritmo di addestramento utilizzo la regressione lineare (LinearRegression).
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
dataset = load_boston()
X=dataset['data']
y=dataset['target']
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
model=LinearRegression()
model.fit(X_train,y_train)
Dopo aver creato il modello con il metodo fit(), lo utilizzo per generare le previsioni sui dati di test (X_test).
p=model.predict(X_test)
Il metodo predict() salva nell'array p le previsioni del modello.
I valori corretti sono invece contenuti nell'array y_test.
Quindi, per valutare la qualità della previsione, devo semplicemente confrontare il vettore delle previsioni (p) con il vettore delle risposte corrette (y_test).
Carico in memoria la metrica (mean absolute error).
from sklearn.metrics import mean_absolute_error
Questa metrica calcola la media del valore assoluto dei residui |y-p| prendendo in input i due vettori.
mae=mean_absolute_error(y_test,p)
Infine stampo il risultato della metrica
print(mae)
Ho così ottenuto una metrica per fare una prima analisi degli errori complessiva e valutare la qualità previsionale del modello.
3.6099040603818047
Se l'indicatore MAE è troppo alto, vuol dire che il modello deve essere perfezionato.
Nota. Le metriche restituiscono soltanto un valore sintetico sulla qualità previsionale. Per comprendere le cause devo svolgere ulteriori indagni più approfondite. Ad esempio, devo cercare di capire in quali caratteristiche (feature) l'errore è più alto.
L'analisi grafica dei residui
Un primo modo per approfondire la distribuzione degli errori è l'analisi grafica degli errori.
Calcolo la differenza tra il valore previsto e il valore target per ogni esempi, ossia il residuo.
res = y_test-p
Poi visualizzo un diagramma cartesiano ponendo il residuo (res) sull'asse delle ordinate e la variabile target (y_test) sull'asse delle ascisse.
Per farlo utilizzo i moduli matplotlib e seaborn
import numpy as np
import seaborn as snp
import matplotlib.pyplot as plt
snp.scatterplot(x=y_test, y=res)
plt.show()
La funzione scaterplot() di seaborn costruisce il diagramma cartesiano mentre la funzione show() di matplotlib lo visualizza.
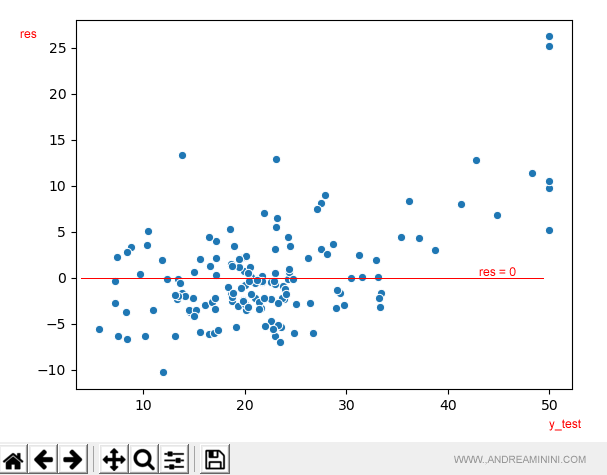
Come si legge?
Ogni punto nel diagramma è un esempio.
I punti vicini all'ordinata res=0 hanno un errore minimo o nullo.
Quanto più un punto è lontano da res=0, tanto maggiore è l'errore.
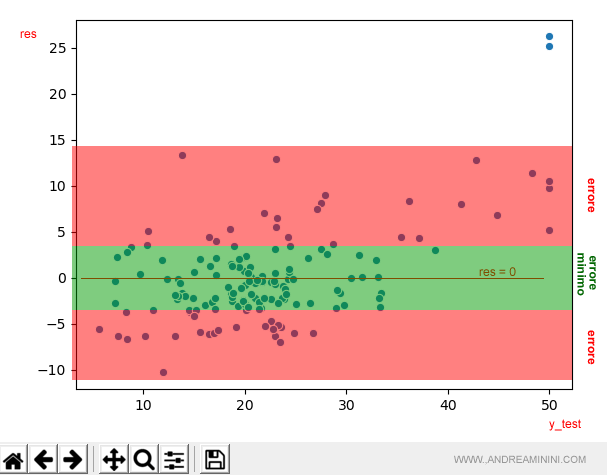
Poichè la variabile target (y_test) è il prezzo, si nota subito che per i prezzi alti (>40) i punti sono pochi e distanti da res=0.
Pertanto, è opportuno aumentare nel dataset gli esempi di questo tipo.
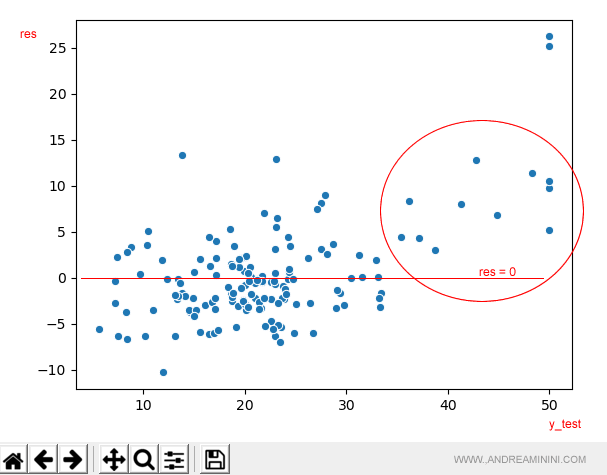
Viceversa, nei prezzi medio-bassi la nuvola dei punti intorno a res=0 è più compatta e l'errore è minore.
Dopo questa prima analisi approfondisco la relazione tra il residuo e le varie features (caratteristiche) del dataset.
L'analisi dei residui rispetto alle singole feature
In questa analisi costruisco lo stesso grafico precedente, sostituendo la variabile target (y_test) con una feature (caratteristica) per indivuare in quali features il modello statistico produce più errori e per quali valori.
Ad esempio, prendo in considerazione il numero delle stanze della casa (room).
Questo attributo si trova alla sesta colonna del dataset. Quindi, estraggo dalla matrice delle features x_test la sesta colonna.
room=X_test[:,[5]]
L'array room ha lo stesso numero di esempi del vettore target (y_test).
Per renderlo confrontabile devo però trasformarlo in un vettore a una dimensione con le funzioni transpose() e reshape() di numpy.
from numpy import transpose, reshape
room=transpose(room)
room=reshape(room,-1)
Poi elaboro un nuovo grafico ponendo il numero delle stanze sull'asse delle ascisse.
I residui restano tali e quali nell'asse delle ordinate.
snp.scatterplot(x=room, y=res)
plt.show()
Questo grafico mette in evidenza la distribuzione degli errori in relazione al numero delle stanze della casa.
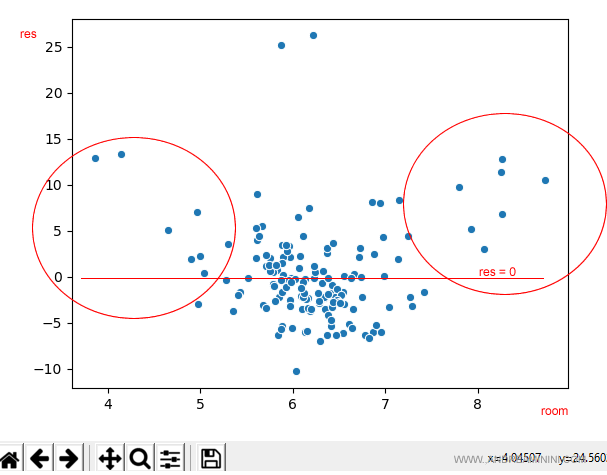
Esempio. Da questa analisi emerge che l'errore del modello si concentra sulle case con con meno di 5 stanze e più di 7 stanze. Potrebbe dipendere dai pochi esempi a disposizione nel dataset di training.
Ripeto la stessa analisi per tutte le features.
Questa indagine mi permette di scoprire le correlazioni tra le features e gli errori.
Una volta raccolti tutti i dati, modifico il dataset ed eventualmente l'algoritmo di addestramento.
Infine, ripeto l'addestramento per produrre un nuovo modello.
E così via.
