La regressione logistica con Sklearn in Python
In questi appunti provo il funzionamento della regressione logistica su scikit-learn di Python.
Cos'è la regressione logistica? Il modello a regressione logistica è un modello di classificazione. E' usato nel machine learning per addestrare un algoritmo a classificare correttamente i dati. Si tratta di un modello lineare di classificazione binaria o multiclasse.
Come funziona la regressione logistica
Il modello di classificazione a regressione logistica prende in input n esempi dall'insieme di training ( X ).
Ogni esempio è composto da m attributi.
Poi elabora una distribuzione di pesi W che sia in grado di classificare correttamente gli esempi tra le varie classi.
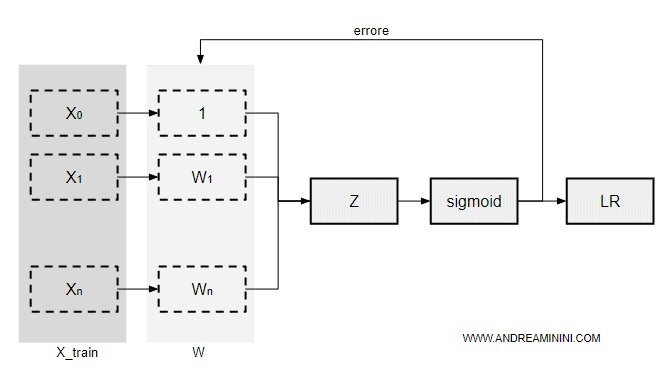
Per ogni campione elabora la combinazione lineare z delle caratteristiche X degli esempi e dei relativi pesi W.
$$ z = x_0 \cdot w_0 + ... + x_m \cdot w_m $$
La combinazione lineare z ( input della rete neurale ) viene passata alla funzione logistica ( sigmoid ) per la classificazione.
$$ φ ( z ) = \frac{1}{1+e^{-z}} $$
La funzione sigmoid calcola la probabilità di appartenenza del campione alle classi.
E' la tipica curva a S della distribuzione delle probabilità.
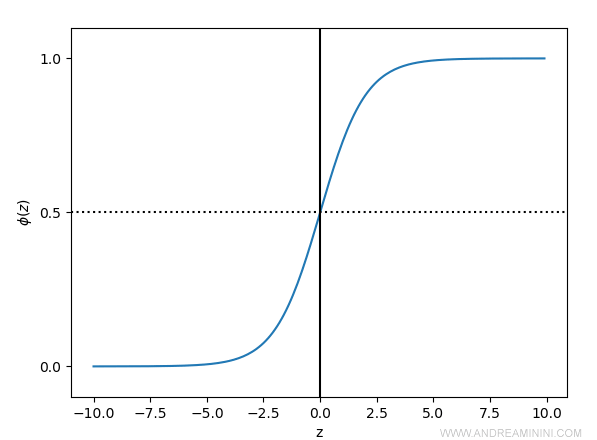
Nota. La classificazione logistica è un modello probabilistico di classificazione. Per ciascuna classe viene calcolata la probabilità di appartenenza del campione. La funzione sigmoid sostituisce la funzione di attivazione già vista in altri modelli più semplici come Perceptron e Adaline.
La regressione logistica in Python
In questo programma addestro il modello di classificazione usando il dataset Iris.
Comincio a scrivere il programma in python caricando i moduli di Scikit-Learn.
- import numpy as np
- from sklearn import datasets
- from sklearn.metrics import accuracy_score
- from sklearn.model_selection import train_test_split
Carico in memoria il dataset Iris.
Suddivido la matrice del dataset in training ( X_train ) e test ( y_train ).
Per semplicità prendo soltanto due attributi su quattro.
- # preparazione dataset
- iris = datasets.load_iris()
- X = iris.data[:, [2, 3]]
- y = iris.target
- X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
Poi standardizzo in scala le variabili del dataset ( X_train_std , X_test_std ).
- # standardizzazione
- from sklearn.preprocessing import StandardScaler
- sc = StandardScaler()
- sc.fit(X_train)
- X_std = sc.transform(X)
- X_train_std = sc.transform(X_train)
- X_test_std = sc.transform(X_test)
A questo punto inizio l'addestramento vero e proprio.
Importo il modello della regressione logistica ( LogisticRegression ) dai modelli lineari di Sklearn.
Imposto gli iperparametri dell'addestramento nell'oggetto lr.
Infine avvio l'addestramento con la funzione fit.
- # addestramento
- from sklearn.linear_model import LogisticRegression
- lr = LogisticRegression(C=1000.0, random_state=0)
- lr.fit(X_train_std, y_train)
Il risultato dell'addrestramento viene registrato nell'oggetto lr.
Dove il parametro C è l'inverso della regolarizzazione.
Pertanto, se riduco il valore C, incremento la regolarizzazione. E viceversa.
Nota. La regolarizzazione è l'adattamento dei dati di training per contenere l'intensità dei pesi, eliminare il rumore nei dati ed evitare il fenomeno dell'overfitting.
Per verificare l'esito del processo di learning, visualizzo le regioni di classificazione dell'insieme di test.
- # visualizzazione grafica della classificazione
- from mlxtend.plotting import plot_decision_regions
- plot_decision_regions(X_test_std, y_test, clf=lr, legend=2)
- import matplotlib.pyplot as plt
- plt.xlabel('petal length [standardized]')
- plt.ylabel('petal width [standardized]')
- plt.legend(loc='upper left')
- plt.show()
Quest'ultima parte di codice mostra graficamente le regioni di classificazione con il modello lr.
Ecco il risultato finale.
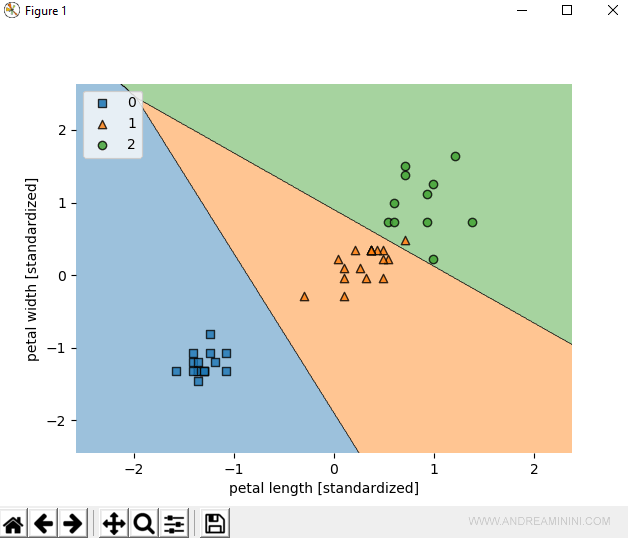
A occhio c'è soltanto un errore di classificazione.
Stampo la lista di tutti i campioni per vedere qual è l'errore.
- for i in range(0,len(X_test_std)):
- z = np.array([X_test_std[i]])
- y = lr.predict(z)
- print((i+1) ,X_test_std[i], y_test[i], y)
L'errore è il campione numero 38.
Il modello LR lo classifica nella classe 2 ( Iris Virginica ) ma l'esempio appartiene alla classe 1 (Iris Versicolor).
| n. | X.train | Y train | Y LR |
|---|---|---|---|
| 1 | [0.70793846 1.51006688] | 2 | 2 |
| 2 | [ 0.09545238 -0.29318114] | 1 | 1 |
| 3 | [-1.35224199 -1.32360858] | 0 | 0 |
| 4 | [1.37610509 0.7372463 ] | 2 | 2 |
| 5 | [-1.29656144 -1.32360858] | 0 | 0 |
| 6 | [1.20906343 1.63887031] | 2 | 2 |
| 7 | [-1.40792255 -1.19480515] | 0 | 0 |
| 8 | [0.48521625 0.35083601] | 1 | 1 |
| 9 | [0.5408968 0.22203258] | 1 | 1 |
| 10 | [0.09545238 0.09322915] | 1 | 1 |
| 11 | [0.98634122 0.22203258] | 2 | 2 |
| 12 | [0.37385514 0.35083601] | 1 | 1 |
| 13 | [ 0.48521625 -0.03557428] | 1 | 1 |
| 14 | [0.42953569 0.35083601] | 1 | 1 |
| 15 | [0.48521625 0.22203258] | 1 | 1 |
| 16 | [-1.35224199 -1.45241201] | 0 | 0 |
| 17 | [0.37385514 0.35083601] | 1 | 1 |
| 18 | [ 0.31817459 -0.03557428] | 1 | 1 |
| 19 | [-1.35224199 -1.19480515] | 0 | 0 |
| 20 | [-1.40792255 -1.06600172] | 0 | 0 |
| 21 | [0.59657735 0.99485316] | 2 | 2 |
| 22 | [0.37385514 0.35083601] | 1 | 1 |
| 23 | [-1.07383923 -1.32360858] | 0 | 0 |
| 24 | [-1.35224199 -1.32360858] | 0 | 0 |
| 25 | [0.5408968 0.7372463] | 2 | 2 |
| 26 | [-1.57496421 -1.32360858] | 0 | 0 |
| 27 | [-1.07383923 -1.06600172] | 0 | 0 |
| 28 | [0.26249403 0.09322915] | 1 | 1 |
| 29 | [-0.29431149 -0.29318114] | 1 | 1 |
| 30 | [-1.24088089 -1.06600172] | 0 | 0 |
| 31 | [0.93066067 0.7372463 ] | 2 | 2 |
| 32 | [0.37385514 0.35083601] | 1 | 1 |
| 33 | [-1.29656144 -1.32360858] | 0 | 0 |
| 34 | [0.59657735 0.7372463 ] | 2 | 2 |
| 35 | [0.98634122 1.25246002] | 2 | 2 |
| 36 | [0.03977182 0.22203258] | 1 | 1 |
| 37 | [-1.18520034 -1.19480515] | 0 | 0 |
| 38 | [0.70793846 0.47963944] | 1 | 2 |
| 39 | [0.20681348 0.35083601] | 1 | 1 |
| 40 | [ 0.09545238 -0.03557428] | 1 | 1 |
| 41 | [0.93066067 1.12365659] | 2 | 2 |
| 42 | [-1.40792255 -1.32360858] | 0 | 0 |
| 43 | [0.70793846 1.38126345] | 2 | 2 |
| 44 | [-1.24088089 -0.80839486] | 0 | 0 |
| 45 | [-1.29656144 -1.32360858] | 0 | 0 |
Il margine di errore della classificazione è del 2,2% ( 1 errore su 45 esempi ).
Come calcolare le probabilità di un campione
Per calcolare la distribuzione delle probabilità di appartenenza alle classi di un singolo campione, o una combinazione particolare degli attributi, posso usare il metodo predict_proba.
Esempio
Ho creato il modello lr e voglio conoscere le probabilità di un campione con attributi 1.2 e 1.6 ( lunghezza e larghezza ).
lr.predict_proba([[1.1, 1.6]])
Il metodo mi restituisce in output le probabilità sulle tre classi.
array([[5.43180413e-13, 1.18153378e-01, 8.81846622e-01]])
In pratica, il campione ha le seguenti probabilità
- 0% (infintesimale) classe 0
- 11.81% classe 1
- 88.18% classe 2
Per vedere le probabilità dei primi dieci campioni dell'insieme di training
lr.predict_proba(X_test_std[0:10, :])
Il metodo restituisce in output un elenco con le probabilità per ciascun campione
array([[1.78177322e-11, 6.12453348e-02, 9.38754665e-01],
[6.52443574e-04, 9.99242776e-01, 1.04780543e-04],
[8.15905531e-01, 1.84094469e-01, 6.46700211e-14],
[1.77343552e-11, 4.15366939e-01, 5.84633061e-01],
[7.98915241e-01, 2.01084759e-01, 1.07274231e-13],
[1.86631492e-13, 1.36009899e-01, 8.63990101e-01],
[8.64521291e-01, 1.35478709e-01, 9.26434600e-14],
[5.04386467e-07, 7.62276348e-01, 2.37723147e-01],
[6.99143083e-07, 8.44028823e-01, 1.55970478e-01],
[8.12729858e-05, 9.97738935e-01, 2.17979244e-03]])
I numeri sono in notazione scientifica esponenziale.
E così via.
