Characteristic Vector of a Petri Net
The characteristic vector of a Petri net N specifies how many times each transition fires within a given sequence σ.
It is also referred to as the associated firing vector.
A practical example
Suppose the net N consists of n=5 transitions:
$$ T = \{ t_1, t_2, ... , t_5 \} $$
Below is its graphical representation:
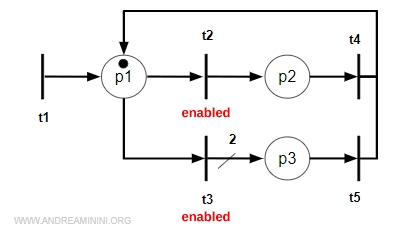
Let's consider one possible transition sequence σ:
$$ σ = t_1 t_2 t_4 t_2 $$
In this sequence, transition t2 fires twice, while t1 and t4 each fire once. Transitions t3 and t5 do not fire at all.
The characteristic vector corresponding to σ is therefore:
$$ σ = [ 1, 2, 0, 1, 0 ] $$
Each entry in the vector represents how many times the corresponding transition occurs.
Note. The first entry corresponds to t1, the second to t2, the third to t3, the fourth to t4, and the fifth to t5. $$ σ = [ t_1, t_2, t_3, t_4, t_5 ] = [ 1, 2, 0, 1, 0 ] $$
And so on.
