Reachability Set in a Petri Net

The reachability set of a Petri net represents all the markings that can be reached from the initial marking M0 through a finite sequence of transitions. $$ R(N,M_0) $$

A Practical Example

Let's look at a simple Petri net with a finite reachability graph.

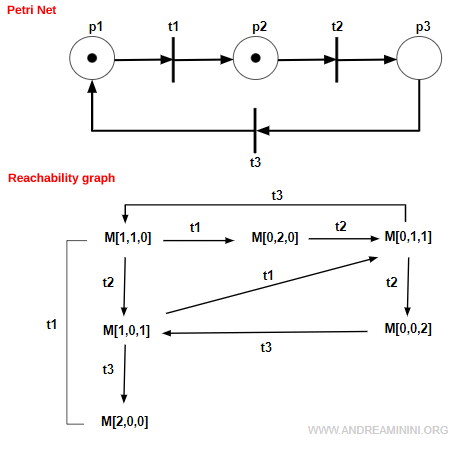
In this example, the markings are defined as follows:

$$ M_0 = [1,1,0] \\ M_1 = [1,0,1] \\ M_2 = [2,0,0] \\ M_3 = [0,2,0] \\ M_4 = [0,1,1] \\ M_5 = [0,0,2] $$

Starting from the initial marking M₀, the reachability set R includes all the markings that the system can evolve into:

$$ R(N,M_0) = \{ M_1, M_2, M_3, M_4, M_5 \} $$

How to Read the Reachability Graph

If the reachability set is finite, we can make several useful observations about the structure and behavior of the Petri net.

• Every reachable marking M corresponds to a node in the reachability graph, and vice versa. In other words, each node represents a possible state of the system. $$ M \in R(N,M_0) \Leftrightarrow \text{M is a node in the graph} $$
• Whenever a marking M belongs to R(N,M₀), there exists at least one sequence of transitions σ=t₁·t₂···t_n that connects M₀ to M. This sequence forms a directed path in the reachability graph and is part of the net's language L(N,M).

  Example. The node M₅ belongs to the reachability set, meaning there is at least one directed path from M₀ to M₅. For instance, the sequence σ=t₁·t₂·t₂ connects M₀ to M₅.
  
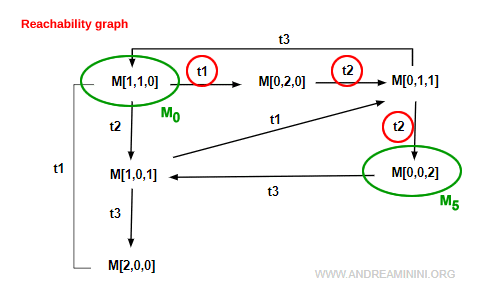
  Multiple paths may exist between the same two markings (for example σ=t₂·t₁·t₂). If the graph contains cycles, the number of possible paths can even become infinite.

• If a marking M' is reachable from another marking M, and M is part of the reachability set R(N,M₀), then M' also belongs to the same set. This relationship ensures that every reachable marking is connected through at least one valid sequence of transitions.

  Example. The marking M₂ can be reached from M₅ via the transition sequence σ=t₃·t₃, which defines a directed path from M₅ to M₂.
  

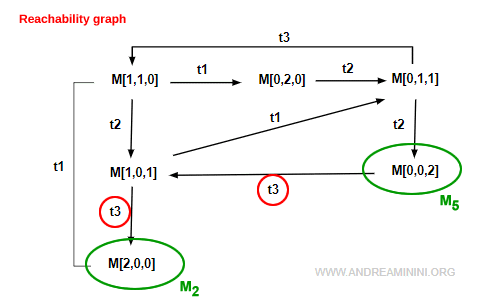
• Whenever a transition t is enabled by a marking M∈R(N,M₀), there will be an outgoing arc from node M labeled with t in the graph.

  Example. In this Petri net, the marking M₁=[1,0,1] enables transitions t₁ and t₃. In the reachability graph, the node M₁=[1,0,1] therefore has two outgoing arcs labeled t₁ and t₃.
  

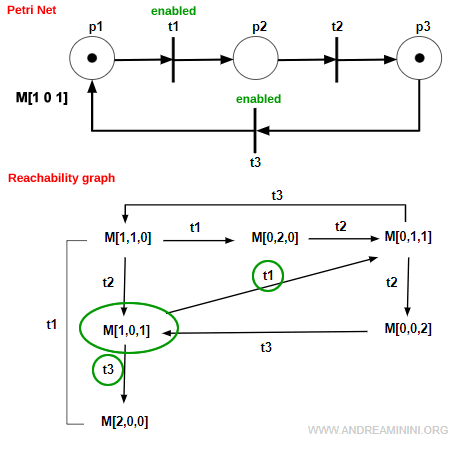
In this way, the reachability graph provides a clear and visual representation of all possible states and transitions in the system, making it an essential tool for analyzing the behavior of a Petri net.