State Equation of a Petri Net

In a marked Petri net <N,M₀>, the state equation shows how the marking of the system changes as transitions occur. It links the initial marking M₀ to the current marking M through the incidence matrix C and the transition sequence σ: $$ M = M_0 + C \cdot σ $$

Understanding the Logic Behind It

Imagine a sequence of transitions σ:

$$ σ = t_{k_1}, t_{k_2}, ... , t_{k_n} $$

Each transition changes the marking of the network:

$$ M_0[σ>M_n $$

The first transition produces marking M₁:

$$ M_0[t_{k_1}>M_1 $$

The second transition gives marking M₂:

$$ M_1[t_{k_2}>M_2 $$

And the process continues until we reach M_n:

$$ M_{n-1}[t_{n}>M_n $$

We can express these updates step by step:

$$ M_1 = M_0 + C \cdot t_1 $$

$$ M_2 = M_1 + C \cdot t_2 \\ M_3 = M_2 + C \cdot t_3 \\ \vdots \\ M_n = M_{n-1} + C \cdot t_n $$

Adding them all together, we obtain the overall result:

$$ M_n = M_0 + \sum_{k=1}^n C \cdot t_{k} $$

This gives us the state equation of the Petri net:

$$ M_n = M_0 + C \cdot σ $$

A Practical Example

Let's take a simple Petri net with an initial marking M₀, three places, and four transitions:

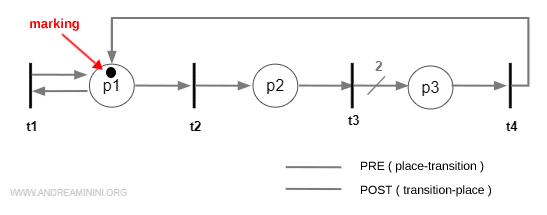
The initial marking is:

$$ M_0 = [ 1 , 0 , 0 ] $$

The incidence matrix C is obtained by subtracting the pre-incidence matrix from the post-incidence matrix:

$$ C = Post - Pre = \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \end{pmatrix} - \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} $$

Now, let's examine a sequence of transitions:

$$ σ = t_1 t_1 t_2 t_3 $$

Here's what happens:

• Transition t₁ occurs twice.
• Transitions t₂ and t₃ occur once each.
• Transition t₄ does not occur.

So, the characteristic vector of this sequence is:

$$ σ = [ 2, 1, 1, 0 ] $$

We can now plug these values into the state equation:

$$ M = M_0 + C \cdot σ $$

Substituting the data:

$$ M = [ 1 , 0 , 0 ] + \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} \cdot [ 2, 1, 1, 0 ] $$

Carrying out the row-by-column multiplication gives:

$$ M = [ 1 , 0 , 0 ] + [ -1, 0, 2 ] $$

$$ M = [ 0 , 0 , 2 ] $$

This means that after firing the sequence t₁t₁t₂t₃, the net reaches the following marking:

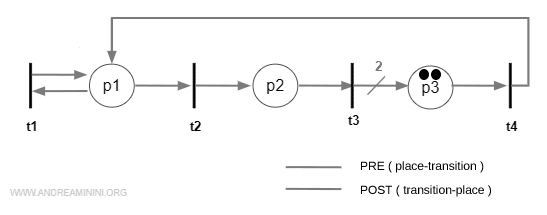
Note. In the final marking, there are two tokens in place p₃ because transition t₃ has two output arcs leading to it.

This simple example shows how the state equation can predict the evolution of a Petri net using linear algebra. It's a powerful way to analyze how tokens move and how the system's state changes over time.