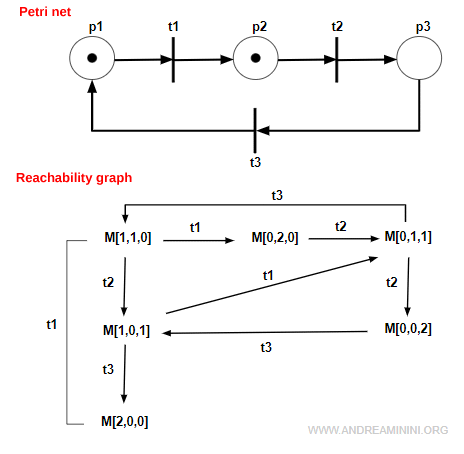
Reachability graph of a Petri net

The reachability graph of a Petri net is the graph of a marked net < n,m₀ > in which each node represents a reachable marking and each arc represents a transition.

In a reachability graph, every reachable marking appears only once as a distinct state.

Transitions may appear several times, because each occurrence corresponds to a firing that is enabled from a specific marking.

Why the reachability graph matters

The reachability graph offers a clear and compact way to explore all possible firing sequences of a Petri net.

It makes the entire state space visible at a glance, showing every reachable marking and how transitions lead from one state to another.

Warning. The reachability graph is a full state-space exploration. Since it includes every possible marking, it becomes infinite if the state space is infinite.

A practical example

Consider a marked net that contains two markings.

The initial marking is M[1,1,0].

In this state, transitions t₁ and t₂ are enabled. Firing them produces the markings [0,2,0] and [1,0,1].

I now begin constructing the reachability graph.

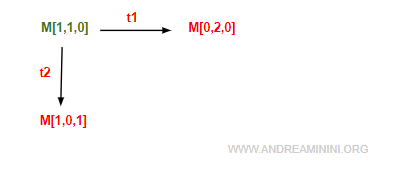
Note. New markings are shown in red. Markings already examined are shown in black so they are not processed again.

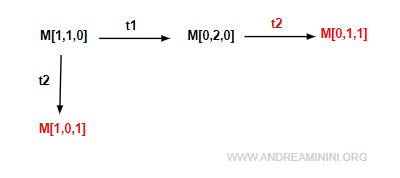
Next, I analyze the marking M[0,2,0].

Only transition t₂ is enabled here, leading to the marking M[0,1,1].

I add this marking to the reachability graph.

I then examine the marking M[1,0,1].

Here, transitions t₁ and t₃ are enabled. They produce the markings [0,1,1] and [2,0,0].

I update the reachability graph accordingly.

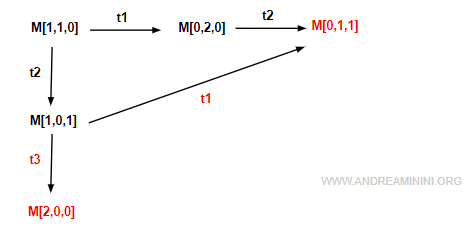
Note. The marking [0,1,1] is already in the graph, so it is not added again. Instead, I simply connect [1,0,1] to it.

I now examine the marking M[0,1,1], where transitions t₂ and t₃ are enabled, producing [0,0,2] and [1,1,0].

I then analyze the marking M[2,0,0], where only transition t₁ is enabled. It leads to [1,1,0].

Finally, I analyze the marking M[0,0,2], where only t₃ is enabled, producing [1,0,1].

 

At this stage, there are no further reachable markings to explore.

The reachability graph of the net is therefore the following:

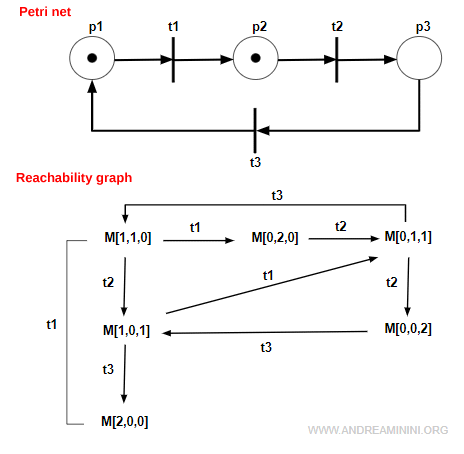
Note. As shown, the reachability graph represents the complete state space of the net. Each marking appears once, while transitions may occur multiple times.

How to build a reachability graph

Given a Petri net with incidence matrix C, you can build the reachability graph by following these steps.

1. Begin by using the initial marking M₀ as the root node of the graph.
2. For each transition enabled by M (that is, when $$ M \ge Pre(*,t) $$), compute M' = M + C(*,t). Add M' to the graph if it does not already exist, and draw an arc from M to M'. Then label M, for example as "ok", to indicate that it has already been processed.
3. Repeat step [2] for each unlabelled node in the graph.

   Note. The algorithm performs one iteration for every reachable marking.

The algorithm stops when all nodes have been processed.

At that point, remove all "ok" labels and the reachability graph is complete.

Warning. If the state space is infinite, the algorithm will not terminate and will run indefinitely.

And so on.