Reachable Markings in Petri Nets
In a marked Petri net, a marking M is called a reachable marking if there exists a firing sequence σ that can transform the initial marking M0 into M. In simple terms, M is reachable if the system can evolve from its starting state M0 to M through a valid sequence of transitions. $$ M_0[σ>M $$
The collection of all markings that can be reached from an initial marking M0 is known as the reachability set (R):
$$ R(N,M_0) $$
This set can be either finite or infinite, depending on how the network is structured and how its transitions interact.
A practical example
Let's look at a simple example. Suppose we have a Petri net with an initial marking M0, two transitions t1 and t2, and three places p0, p1, and p2.
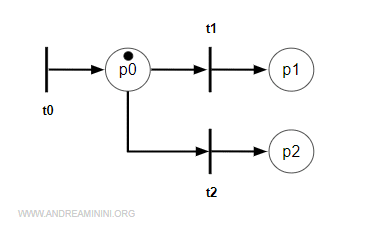
The reachability set starting from M0 is:
$$ R(N,M_0) = \{ M_0, M_1, M_2 \} $$
which can be written explicitly as:
$$ R(N,M_0) = \{ [1,0,0], [0,1,0], [0,0,1] \} $$
The marking M0 = [1,0,0] can be reached through one or more empty transitions ε - transitions that do not actually change the state of the net.
Note. An empty transition ε leaves the net's marking unchanged, yet it is still considered an enabled transition. $$ M_0[ε>M_0 $$
The marking M1 = [0,1,0] is reached when transition t1 fires, while M2 = [0,0,1] occurs when transition t2 fires.
So, the possible behaviors of the net starting from M0 can be represented as:
$$ L(N,M_0) = \{ e, t_1, t_2 \} $$
Note. In this particular net, no single sequence of transitions can pass through all reachable markings from M0. For instance, if transition t2 fires, the system moves to place p2, where transition t1 is no longer enabled - and vice versa.
In summary, the concept of reachability helps us understand how a Petri net can evolve over time, which states can actually be achieved, and which are impossible under its current configuration.
