How a Transition Fires in a Petri Net
In a Petri net, a transition that’s enabled by a marking M can fire. The firing of a transition t creates a new marking M′ that replaces the old one: $$ M' = M - Pre(*,t) + Post(*,t) \\ = M + C(*,t) $$
When a transition fires, tokens are taken from its input places and placed into its output places. This changes the state of the system, represented by the new marking M′.
The firing process is usually written as:
$$ M[t>M' $$
Note. The matrix C is the algebraic difference between the Post and Pre matrices: $$ C = Post - Pre $$
A Simple Example
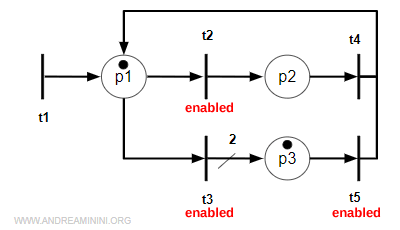
In the Petri net below, transition t2 is enabled because there’s a token in place p1.
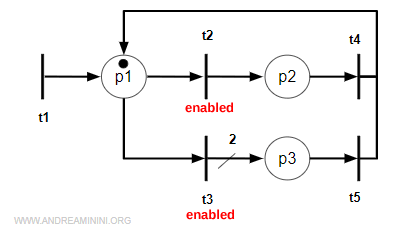
When t2 fires, the token moves from p1 to p2.
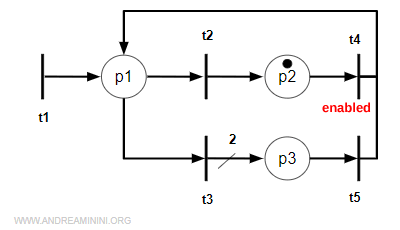
Now transition t4 becomes enabled, since the token is sitting in p2.
$$ M' = M - Pre(*,t) + Post(*,t) = 1 - 1 + 1 = 1 $$
Note. If transitions t1, t3, t5, or even t2 were to fire at this moment, nothing would happen - the token would stay in p2. The marking only changes when an enabled transition fires. However, as the system evolves, other transitions that are currently disabled may later become enabled.
When t4 fires, the token returns to p1.
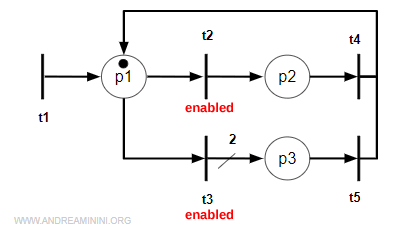
Let’s see what happens with transition t3.
Transition t3 is also enabled, but it connects to place p3 through two output arcs instead of one.
$$ M' = M - Pre(*,t) + Post(*,t) = 1 - 1 + 2 = 2 $$
This means that when t3 fires, it moves the token and duplicates it in p3.
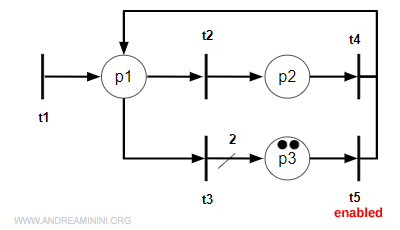
When t5 fires, only one token moves back to p1 (since there’s just one output arc), while the other token stays in p3.
And the process keeps repeating - firing, moving, and transforming the net’s state step by step.
