Structural conflict transitions in Petri nets
In a Petri net, two transitions t and t' are said to be in structural conflict when they share at least one common input place. In practical terms, this happens when a place has outgoing arcs to both transitions. Formally: $$ *t ⋂ *t' ≠ 0 $$
The notation *t refers to the set of input places of transition t, while *t' refers to the input places of transition t'.
Example. The input sets *t1={p0} and *t2={p0} clearly share the same input place, p0.
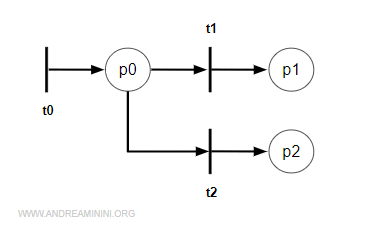
However, the mere presence of a shared input place does not automatically imply that a real conflict will occur during execution.
To understand what actually happens at runtime, structural conflicts can be divided into two categories: effective and non effective conflicts.
-
Effective structural conflict. Two transitions are in an effective conflict under a marking M if both transitions are enabled, but the available tokens in their input places are not sufficient to satisfy the weights of the incoming arcs. Formally: $$ M < Pre(*,t)+Pre(*,t') $$
In this situation, there are not enough tokens to allow both transitions to fire. As a result, only one of them can proceed.
Example. Under the marking M[1,0,0], both t1 and t2 are enabled, but they are in effective conflict. There is only one token available, and it cannot authorize the firing of both transitions at the same time.
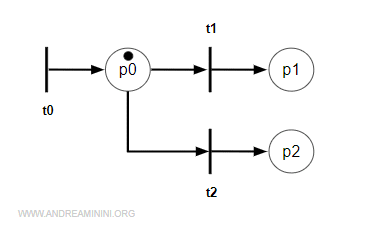
Both transitions depend on the same input place p0. $$ M = 1 \ge Pre(*,t_1) = 1 \\ M = 1 \ge Pre(*,t_2) = 1 $$ Yet, that single token is not enough to satisfy both transitions simultaneously: $$ M = 1 \ge Pre(*,t_1) + Pre(*,t_2) = 2 $$ -
Non effective structural conflict. Two transitions are in a non effective structural conflict under a marking M if both are enabled and their input places contain enough tokens to satisfy the weights of the arcs leading to the transitions. Formally: $$ M \ge Pre(*,t)+Pre(*,t') $$
In this case, both transitions can fire without preventing each other from executing.
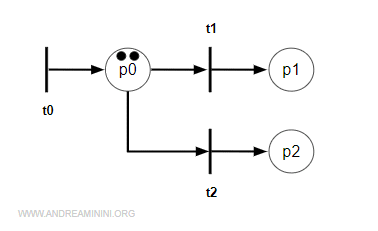
Example. When M contains two tokens, the conflict is not effective, because there are enough resources to trigger both t1 and t2.
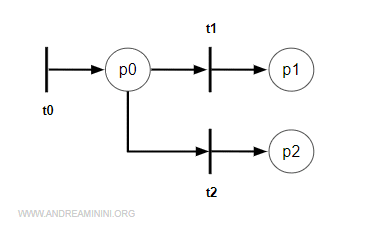
Example 2. In the scenario below, transitions t1 and t2 are not enabled by p0. As a result, no effective conflict occurs.
To sum up, an effective structural conflict depends not only on the static topology of the net, but also on the current marking of the places, which determines whether transitions can actually fire.
And so on.
