Labeled Petri Nets

A labeled net is a marked Petri net <N, M₀> equipped with a labeling function l:T→E. The function assigns each transition t ∈ T a symbol l(t) from the event alphabet and defines a set of final markings. $$ N_L = < N, M_0, l, F > $$

The key idea is simple. Instead of listing transitions one by one, the labeling function lets us represent an entire firing sequence as a single word w built from the alphabet E.

Petri Languages

A Petri net allows only certain sequences of transitions. These sequences form the language of enabled transitions:

$$ L(N, M_0) $$

The generated language is the set of all firing sequences that can start from the initial marking:

$$ L(N_l) $$

The accepted language is more restrictive. It includes only the enabled sequences that also reach a final marking.

A Practical Example

Consider the Petri net below, which models a simple warehouse workflow.

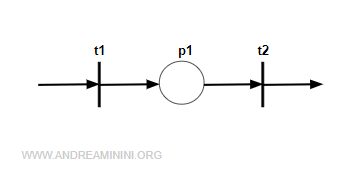
For clarity, the warehouse has no capacity limit and starts empty. The net uses two transitions:

• t₁ stores one unit in the warehouse. Each time it fires, it adds a token to place p₁.
• t₂ removes one unit from the warehouse. It can fire only if p₁ contains at least one token.

The labeling function assigns symbol "a" to t₁ and symbol "b" to t₂:

$$ l(t_1) = a \\ l(t_2) = b $$

The resulting event alphabet is:

$$ E = \{ a, b \} $$

Here, the final marking F corresponds to an empty warehouse. From this setup we obtain two languages. The generated language includes all words w where the number of a symbols is greater than the number of b symbols:

$$ aba \\ aab \\ aba \\ abaa \\ ababa \\ \vdots $$

The accepted language includes only the words w with an equal number of a and b symbols:

$$ abab \\ aabb \\ abab \\ abaabb \\ ababab \\ \vdots $$

Petri Languages and Automata

Petri languages cover a broad class of behaviors, including both regular and non-regular languages.

All regular languages fit inside the family of Petri languages. This means any automaton can be modeled by a Petri net by mapping each state x to a place in the net.

However, the opposite is not always possible. Petri nets can describe systems and languages that go beyond the expressive power of regular automata.