Enabled Transitions in a Petri Net
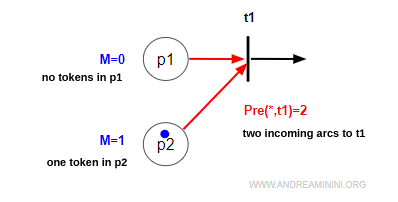
In a Petri net, a transition (t) is considered enabled when all its input places contain enough tokens to “fire” the transition. In other words, every place feeding into that transition must have a number of tokens M that is at least equal to the number of incoming arcs to it, represented by Pre(*,t). Mathematically, this is expressed as: $$ M \ge Pre(*,t) $$
Here, M is the number of tokens in the input place, and Pre(*,t) represents how many arcs connect that place to the transition.
When a transition is enabled, we write it as:
$$ M[t> $$
If it’s not enabled, it’s written as:
$$ ¬ M[t> $$
Example: How to identify an enabled transition
In the Petri net below, transitions t1 and t2 are enabled - meaning they can “fire.”
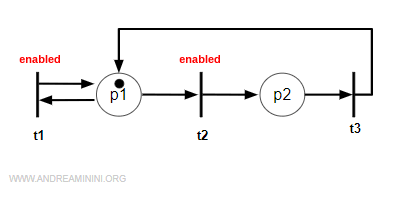
Explanation. Transition t1 has one incoming arc (Pre(*,t1)=1), and its input place p1 contains one token (M=1). The same goes for t2. In contrast, transition t3 is not enabled because its input place p2 has no tokens (M=0), even though it has one incoming arc (Pre(*,t3)=1).
Another case: multiple input places
In the next example, transitions t2 and t3 are enabled, but t4 is not. That’s because t4 has two input arcs (Pre(*,t4)=2), and neither of its input places (p2 and p3) has enough tokens to satisfy M≥2.
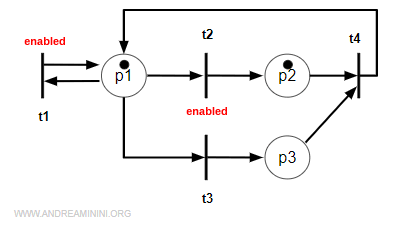
Note. Transition t4 becomes enabled only if all its input places (p2 and p3) meet the requirement M≥2. It’s not enough for just one of them to meet it - they all must.
Special case: source transitions
A source transition is a special type of transition with no incoming arcs at all:
$$ Pre(*,t)=0 $$
Because of that, it’s always enabled - there are no input conditions to block it. Formally,
$$ M \ge Pre(*,t)=0 $$
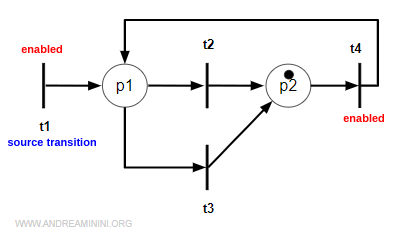
Example. In the Petri net below, transitions t1 and t4 are enabled. Transition t1 is a source transition, meaning it has no incoming arcs (Pre(*,t1)=0). The enabling condition M≥Pre(*,t1) is therefore automatically satisfied, since M=0 and Pre(*,t1)=0, which means M≥0.
In summary
Enabled transitions are the key to understanding how a Petri net evolves. Whenever the enabling condition is met, the transition can fire - moving tokens from input places to output places - and the system changes state. Recognizing these transitions helps you analyze and predict the behavior of any Petri net, from simple models to complex distributed systems.
